1. Алгебра
  2. Сумма двух корней уравнения равна

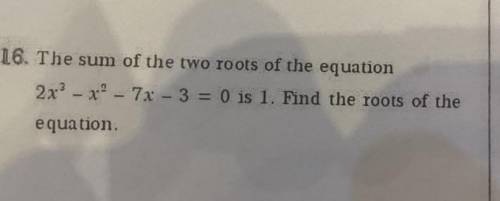
Сумма двух корней уравнения равна 1. Найдите корни уравнения.


Сумма двух корней уравнения равна 1. Найдите корни уравнения.

Россия111111111111 Россия111111111111    3   19.06.2020 22:08    2

Ответы
taylakova63p06vpw taylakova63p06vpw  15.10.2020 14:29

\frac{1\pm\sqrt{13}}{2}, -\frac{1}{2}

Объяснение:

Пусть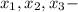 x_1,x_2,x_3 - корни кубического уравнения и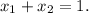 x_1+x_2 = 1.

Тогда для каждого из корней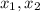 x_1,x_2 выполняются равенства:

2x^3_1 - x^2_1 - 7x_1 - 3 =0;

2x^3_2-x^2_2-7x_2-3=0;

Сложим эти два равенства:

2(x_1^3+x_2^3) - (x_1^2+x_2^2) - 7(x_1+x_2) - 6 = 0;

2(x_1+x_2)(x_1^2-x_1x_2+x^2_2) - ((x_1+x_2)^2 - 2x_1x_2) - 7(x_1+x_2)-6=0;

2(x_1+x_2)((x_1+x_2)^2-3x_1x_2)-((x_1+x_2)^2-2x_1x_2)-7(x_1+x_2)-6=0;

С учетом равенства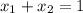 x_1+x_2=1 имеем:

2(1-3x_1x_2)-(1-2x_1x_2)-7-6=0;

2-6x_1x_2-1+2x_1x_2-13=0;

4x_1x_2 = -12;

x_1x_2=-3;

По теореме, обратной теореме Виета,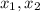 x_1,x_2 - корни квадратного уравнения:

x^2 -x-3 =0;

Решая это уравнение, имеем:

x_1 = \frac{1+\sqrt{13}}{2}, x_2 = \frac{1-\sqrt{13}}{2}

Исходный кубический многочлен можно представить в виде:

2x^3 - x^2 -7x - 3 = 2(x-x_1)(x-x_2)(x-x_3);

2x^3 - x^2 - 7x - 3 = 2x^3 -2(x_1+x_2+x_3)x^2+2(x_1x_3+x_2x_3+x_1x_2)x-2x_1x_2x_3.

Два многочлена тождественно равны, если равны коэффициенты при соответствующих степенях. Тогда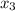 x_3 можно найти, например, из условия

x_1+x_2+x_3 = \frac{1}{2} = 1+x_3 = \frac{1}{2} = x_3 = -\frac{1}{2}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Nastyusha2aa5 Nastyusha2aa5  22.10.2019 21:26
Щоб насипати в кожен пакет по 3 кг борошна, не вистачає 20 кг борошна. коли в кожен з пакетів насипали по 2 кг борошна, залишилося не розфасовано ще 60 кг. скільки пакетів...
annafilimonova1 annafilimonova1  22.10.2019 21:24
Задумали число, если к этому числу прибавить 12 полученную сумму умножить на 5,а из произведения вычесть 16, то получиться задуманное число...
holil070707325 holil070707325  22.10.2019 21:24
Надо вместе с рисунком 2 sinx cos x = -1...
follizy follizy  22.10.2019 21:24
8класса новый учебник мордковича​...
missislevitina missislevitina  22.10.2019 21:23
Числовые неравенства. системы и совокупность линейных неравенств с одной переменной. решение двойных неравенств. хотя бы что знаете...
kravcukpolap08qwd kravcukpolap08qwd  22.10.2019 21:23
Известно, что сумма 625++625 равна 5 в 101 степени. сколько слагаемых в этой сумме. с объяснением, ! ​...
Denchik01TURBO Denchik01TURBO  22.10.2019 21:20
Найдите значение выражения7х+25у при х=3/7, у=-1/5​...
ЕваКротевич ЕваКротевич  20.09.2019 08:20
Решить этот сложнейшее уравнение, не помню как решать x^2=-x...
патишка1 патишка1  20.09.2019 08:20
Знайдіть ймовірність того, що навмання взяте двоцифрове число виявиться кратним 25...
taton92p08oqp taton92p08oqp  20.09.2019 08:20
Найдите значение выражения п ри a= _-1_ 12...

Популярные вопросы