Стрелок производит 4 выстрела. вероятность попадания в мишень при каждом выстреле равна 0,45. за каждое попадание стрелку засчитывается 5 очков. построить ряд распределения числа выбитых очков. описать полностью действия с формулой.
Другие вопросы по теме Алгебра
Популярные вопросы
- Пришли Святополк, и Владимир, и Давыд Игоревич, и Василько Ростиславович,...
1 - Хто напише двм ІВ Виписати прислів я,які б виражали ідею твору....
1 - Fill in many/much.He always asks questions.Has she got books?I...
1 - Магний взаимодействовать с каждым из двух веществ: 1) алюминий...
1 - Определите часть речи каждого слова в данных предложениях (части...
2 - Почему германское командование оказывало сопротивление на восточном...
1 - Вокально - інструментальний твір для соліста з фортепіанним супроводом...
3 - Структуру сукупність даних, розміщених по рядках і стовпцях А)...
1 - Розподіліть і запишіть у три колонки прикметники відповідно до...
3 - 13. Сколько в данном тексте предложений?начало весны у волчицы...
3
Пусть случайная величина X - число выбитых очков; также добавим что эта случайная величина распределена по биномиальному закону.
1) Стрелок выбил 0 очков, т.е. он не попал ни разу в мишень. Такова вероятность будет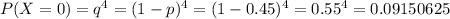
2) Стрелок выбил 5 очков, т.е. в мишень он попал один раз. Вероятность того, что при 4 выстрелах стрелок попадет только один раз, равна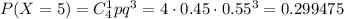
3) Стрелок выбил 10 очков, т.е. в мишень он попадает два раза. Вероятность того, что при четырех выстрелах стрелок попадет ровно два раза равна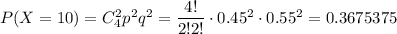
4) Стрелок выбил 15 очков, т.е. в мишень стрелок попал три раза. Вероятность того, что при 4 выстрелах стрелок попал ровно 3 раза равна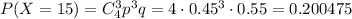
5) Стрелок выбил 20 очков, т.е. он в мишень попал ровно 4 раза. Такова вероятность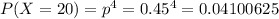
Закон распределения случайной величины X:
Xi 0 5 10 15 20
Pi 0.09150625 0.299475 0.3675375 0.200475 0.04100625