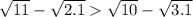Сравнить числовые значения выражений: 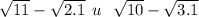
П.с : я знаю, что можно возвести в квадрат, но мне нужно другим решить, так что РЕШИТЕ ДРУГИМ И КАК МОЖНО ПРЯМ ПОДРОБНО
Другие вопросы по теме Алгебра
Популярные вопросы
- В арифметической прогрессии Вычислите ...
3 - Прочитайте текст и выполните задания Колыбель тюркского мира Большое значение...
1 - СОР 8 класс 2 вариант 1. Выберите правильный вариант ответа: (a) Закон Авогадро...
3 - Заполните таблицу сделайте вывод об исторической значимости становления национальных...
2 - Уравнение (X+ 364) * 123 11364...
3 - 1. Mark don’t like salad. 2. Bella eat watermelon. 3. Does they live in Kazakhstan?...
3 - выберите функции графики которых параллельны ответ обоснуйте y=0,5 + 8 и у =...
3 - Tick (+) the correct sentence....
3 - за правильный ответ Выпиши прилагательные с текста Мы все спешим за чудесами,...
3 - Сократите дробь: x^2-10x+16/8-x (/-это дробь)...
2
Рассмотрим функцию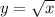 . Она является возрастающей на всей области определения, то есть большему значению аргумента соответствует большее значение функции.
. Она является возрастающей на всей области определения, то есть большему значению аргумента соответствует большее значение функции.
Рассмотрим числа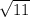 и
и 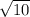 . Зная, что
. Зная, что 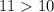 и в силу монотонности функции корня, получим, что
и в силу монотонности функции корня, получим, что 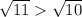 .
.
Рассмотрим числа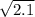 и
и 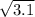 . Зная, что
. Зная, что 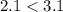 и в силу монотонности функции корня, получим, что
и в силу монотонности функции корня, получим, что 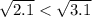 .
.
Обе части неравенства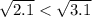 домножим на (-1), изменив знак неравенства:
домножим на (-1), изменив знак неравенства:
Наконец, сложим два неравенства одного смысла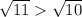 и
и 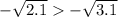 :
:
Другими словами, рассмотрев первое выражение и второе выражение
и второе выражение  , можно заключить следующее. Первое выражение имеет большее уменьшаемое, чем второе выражение. Также первое выражение имеет меньшее вычитаемое, чем второе выражение. Значит, первая разность больше второй.
, можно заключить следующее. Первое выражение имеет большее уменьшаемое, чем второе выражение. Также первое выражение имеет меньшее вычитаемое, чем второе выражение. Значит, первая разность больше второй.
ответ: