Sqrt(cos^2 x + cos x)/(sin x) + 1 = 0

Другие вопросы по теме Алгебра
Популярные вопросы
- Rsa — криптографическая система, где важную роль играют числа...
3 - Составьте 5 предложений с приложениями, которые называют столицы...
1 - Задать вопросы к: 1. ja, das bild ist nett. 2. erist arbeiter....
3 - Утрикутнику abc ab= 1 см, bc=[tex] \sqrt{2} [/tex]см, ∠a= 135°....
3 - Ничего не понял но интересно p.s отмеченные уже сделаны...
1 - На данной прямой находятся точки m(-1; -2) и n(0; 2). определи...
3 - Разбирать предложение: маше пора выходить замуж...
3 - При каком наименьшем значении переменной t выражения (t²-++13)...
3 - Найдите корень уравнения кос •п(4х-1)/4 =корень 2/2...
3 - 1. постройте график функций y=x²-2x, если d(y)=[-2; 1] 2 постройте...
1
ответ: а)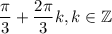
б)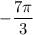
Объяснение:
С учетом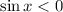 :
:
б)
Объяснение:
Всё подробно написала в решении.