Составьте уравнение касательной к графику функции y=x^4-2x^2-8 в точках его пересечения с осью абцисс. найдите точьку пкресечения этих касательных
Другие вопросы по теме Алгебра
Популярные вопросы
- Давление в газосветной трубке, заполненной неоном, составляет 104 Па. Определить...
2 - отвечу как лучший и поставлю ЗАДАНИЕ 1: ВСТАВЬТЕ ПРОПУЩЕННЫЕ СЛОВА. ( ) Вода...
1 - Выпишите из текста предложение , отражающее его основную мысль . В какой...
3 - Составьте уравнения практически осуществимых реакций. Укажите условия осуществления...
2 - каким образом Мазепа хотел отомстить Петру? получилось у него это или нет?...
3 - Составить хим реакцию и объяснить её❤️ )...
2 - РЕБЯТА , ОЧЕНЬ СРРЧНО ! КОНТРОЛЬНАЯ РАБОТА...
1 - Прочитайте текст и выполните задания. Есть ценности, которые теряются. Но...
2 - На рисунке изображено строение атома кислорода (О). Подпишите названия элементарных...
1 - это соч по литературе только Прочитайте отрывок из повести Н.В. Гоголя «Ночь...
3
Найдём точки пересечения с осью х
не подходит, т.к.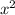 не может быть отрицательным числом
не может быть отрицательным числом
Уравнение касательной
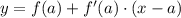
Производная функции
Пусть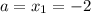
Тогда
Уравнение касательной
Пусть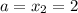
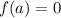
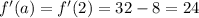
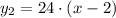
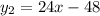
Тогда
Уравнение касательной
Приравняем правые части функций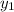 и
и 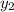 , чтобы найти точку их пересечения
, чтобы найти точку их пересечения
-24x-48 = 24x-48
х = 0
Точка пересечения имеет координаты (0; -48)