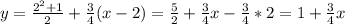Составьте уравнение касательной к графику функции у= х^2 +1 / х в точке х0=2
Другие вопросы по теме Алгебра
Популярные вопросы
- Наклонная AD с плоскостью α образует угол 300, а наклонная DC с плоскостью...
1 - Тема: Kindergartens 1. Переведите текст, запишите перевод This kindergarten...
1 - Какие функции из предложенных выполняет город Москва мне очень надо :((...
1 - НУЖНО РЕШИТЬ ВСЕ 623,624,625 ВСЕ НУЖНО РЕШИТЬ ТОЛЬКО В ТЕТРАДИ РЕШИТЕ...
1 - До розчину солі двовалентного металу додали 6 г магнію, який повністю...
2 - Дано:AB=CD Доказать:OK=OP...
1 - Коник-стрибунець відштовхується від землі вертикально вгору з швидкістю...
2 - 1. Хто такий Валерій Кікта?2. Який твір створив Валерій Кікта?3. Під...
2 - Причина активного господарського освоєння степової зони людиною...
3 - ЛЮДИ Как удалить фото на рэш???...
1
Объяснение:
Производная функции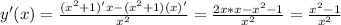
В точке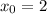
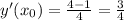
Уравнение касательной