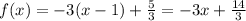Составьте уравнение касательной к графику функции у=5/3x^3/5 + x^-4 , в точке х=1
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите сочинение на тему, первый раз в музее,...
1 - Написать уравнение реакции взаимодействия а) с naoh 4-аминогексановой кислоты...
3 - Описание картины, используя неполные предложения (картина кустодиева ,,сенокос»)...
2 - 5. цілком серйозно. щоб з ясувати істину, карл шееле скуштував синильну кислоту...
3 - Предложения по вопросам пенсионного фонда российской федерации. распишите более...
2 - Вячейке а3 записано значение радиуса r=5.6.запишите в ячейку а4 и а5 формулы расчета...
1 - Перевести на , учитывая притяжательные. . 1. в витрине магазина было много мужских...
1 - Сделайте план характеристики реки дунай план: 1.определите,на каком материке и...
1 - Определить причастный оборот во всех...
2 - Решите . не поняла тему. заранее большое !...
2
Общий вид уравнения касательной: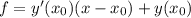
Вычислим значение функции в точке х0=1, т.е.
Найдем теперь производную функции и затем найти ее значение в т. х0=1
Уравнение касательной