составьте таблицу значений функции
для целых значений аргумента х если
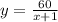
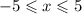
Другие вопросы по теме Алгебра
Популярные вопросы
- Посилення русинського напряму в українському русі Галичини відбулося...
2 - Виправити помилку, переробити на складне // просте речення з ускладненням....
3 - Представьте числа -1 ; 5 в тригонометрической форме комплексного...
3 - Переложите свойства воды в пятих ...
3 - Анализ стихотворения Помню долгий зимний вечер 1 . О чём стихотворение?2....
1 - Я очень давно хотела съездить в москву . и наконец-то мне удалось...
3 - Факторы расселения населения и Конкретные примеры населенных пунктов!!...
1 - Отзыв на произведенье Приёмыш...
1 - Фонетика как раздел лингвистики речи и буквы алфавит00...
3 - поле шахматной доски определяется парой натуральных чисел каждое...
3
В решении.
Объяснение:
ОДЗ: