1. Алгебра
  2. Составьте квадратное уравнение,

Составьте квадратное уравнение, каждый корень которого в 7 раз больше соответствующего корня уравнения 4x^2-15x+2=0​

lisena123409 lisena123409    2   12.12.2019 22:15    54

Ответы
360Polina360 360Polina360  10.10.2020 20:19

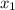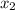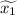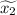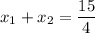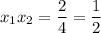Обозначим корни исходного уравнения как x_1 и x_2, а корни нового как \widetilde{x_1} и \widetilde{x_2}. По теореме Виета x_1+x_2=\dfrac{15}{4} и x_1x_2=\dfrac{2}{4}=\dfrac{1}{2}. Тогда получим:

\widetilde{x_1}+\widetilde{x_2}=7x_1+7x_2=7(x_1+x_2)=7 \cdot \dfrac{15}{4}=\dfrac{105}{4}\\\widetilde{x_1} \cdot \widetilde{x_2} =7x_1 \cdot 7x_2=49 \cdot x_1x_2=\dfrac{49}{2}

Теперь можем составить уравнение по коэффициентам, пользуясь обратной теоремой Виета:

x^2-\dfrac{105}{4}x+\dfrac{49}{2}=0\\4x^2-105x+98=0

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
tolikbn85 tolikbn85  11.12.2020 12:03
Буду благодарен если решите. В деревне Матитика вдоль прямой дороги живут (в указанном порядке) пять подружек: Аля, Белла, Валя, Галя и Диля. Каждая из них нашла сумму расстояний...
Nasya156 Nasya156  11.12.2020 12:04
На поле игры «Сапёр» в некоторых клетках стоит по одной мине. В остальных клетках расставлены числа, равные количеству мин в соседних (по стороне или углу) клетках. На поле...
striletsnastya striletsnastya  11.12.2020 12:05
Вынеси за скобки общий множитель...
marvin4547 marvin4547  11.12.2020 12:06
Два робітники, працюючи разом, можуть виконати завдання за 8 днів. Перший робітник, працюючи один, може виконати роботу в 2 рази швидше, ніж другий. За скільки днів виконає...
Ler4ic004 Ler4ic004  23.05.2019 16:30
Что в значит знак € только с одной палочкой ?...
FarLime FarLime  23.05.2019 16:30
Найдите любые три решения уравнения 7х-8у=1...
vikaprostitova vikaprostitova  23.05.2019 16:30
2х-3=5 ривносильне ривняння а) 2х=5+3 б) 2х=5-3 в)2х=5*3...
sgymgjvb sgymgjvb  23.05.2019 16:30
На весенней распродаже в магазине товар стоимостью 350 р. уценили на 40% а через неделю еще на 5%. в супермаркете такой же товар уценили на 5% а через неделю еще на 40%. а на...
AwesomeLeva AwesomeLeva  23.05.2019 16:30
Запишите в ответы номера верных равенств а^2-10а+25=(а-5)^2, 25-а^2=(5+а)(а-5), (b-1)(a-5)=-(1-b)(a-5), (a+1)(2a-5)=2a^2+2a-5...
mailnadejda mailnadejda  23.05.2019 16:30
Вкабинете в шкафу стояли учебники по и . количество учебников по состовляло 3/5 от количеста учебников по , а затем добавить 6 учебников по , то книг по этим предметам станет...

Популярные вопросы