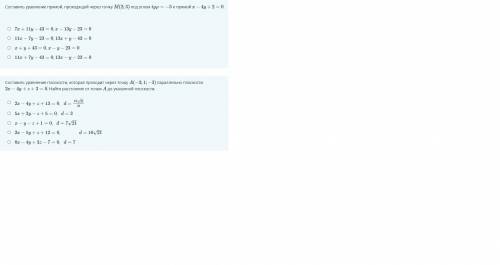
Составить уравнение прямой, проходящей через точку M(2;3) под углом tgφ=−3 к прямой x−4y+2=0. и второе во вложении

Объяснение:

x-4y+2=0       M(2;3)      tgα=-3.

Запишем прямую х-4у+2=0 в виде уравнения у=kx+b с угловым коэффициентом k:

Значит угловой коэффициент данной прямой k=0,25.

Геометрический смысл углового коэффициента:  

k=tg α,  где α– угол наклона прямой у=kx+b c положительным направлением оси Ох.

При пересечении двух прямых  у=k₁x+b₁ и у=k₂x+b₂:   k₁=tg α₁,  k₂=tg α₂,

а угол между прямыми  α=α₁–α₂.         ⇒            

По формуле тангенса разности двух углов:

ответ: 13x-y-23=0.

1 .Угловой коэффициент данной прямой к₁=1/4, т.к. у=х/4+1/2;

угловой коэффициент - это тангенс угла наклона прямой с положительным направлением оси абсцисс.

к₂=-3, угол пересечения прямых β связан с к₁ и к₂ уравнением

tgβ=(к₁-к₂)/(1+к₁*к₂)=(1/4-(-3)/(1+(1/4)*(-3))=(13/4)*4=13, искомая прямая имеет вид у=13х+b, найдем b, используя условие прохождения этой прямой через точку М(2;3)

3=2*13+b,⇒b=-23; или в общем виде 13х-у -23=0

ответ  последний в списке ответов. 13х-у -23=0

2. нормальный вектор данной плоскости →n(2;-4;1)

т.к. плоскости - данная и искомая - параллельны, то  нормальным вектором искомой плоскости тоже будет вектор →n(2;-4;1), уравнение искомой плоскости запишем в виде

2*(х-(-3))-4*(у-1) +1*(z-(-3 ))=0, или после упрощения

2х+6-4у+4+z+3=0

2х-4у+z+13=0 - первый в списке ответов.

расстояние от точки  А(-1; 3; -1) до плоскости 2х-4у+z+3=0 найдем по формуле расстояния  от точки А(х;у;z) до плоскости ах+bу+сz+d=0;

d =  |а·Аx +b·Аy + c·Аz + d|/√(а²+b² +c²)

d=I2*(-3)-4*1+1*(-3)+3I/√(2²+(-4)²+1²)=10/√21=10√21/21

ответ

2х-4у+z+3=0

10√21/21