Составить уравнение окружности с центром в точке (-3; 8), диаметр которой равен фокусному расстоянию эллипса x^2/100+y^2/36=1 :
Ответы
Фокусное расстояние эллипса равно 2*с, где 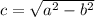 , пр этом а²=100, b²=36, отсюда с=8, а фокусное расстояние F=2*с=16, радиус окружности R=8. Уравнение окружности радиуса R с центром в произвольной точке A(a,b) записывается как (x−хц)²+(y−yц)²=R²., здесь хц yц - координаты центра. То есть искомое уравнение окружности (x+3)²+(y-8)²=8².
, пр этом а²=100, b²=36, отсюда с=8, а фокусное расстояние F=2*с=16, радиус окружности R=8. Уравнение окружности радиуса R с центром в произвольной точке A(a,b) записывается как (x−хц)²+(y−yц)²=R²., здесь хц yц - координаты центра. То есть искомое уравнение окружности (x+3)²+(y-8)²=8².
ПОКАЗАТЬ ОТВЕТЫ
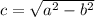 , пр этом а²=100, b²=36, отсюда с=8, а фокусное расстояние F=2*с=16, радиус окружности R=8. Уравнение окружности радиуса R с центром в произвольной точке A(a,b) записывается как (x−хц)²+(y−yц)²=R²., здесь хц yц - координаты центра. То есть искомое уравнение окружности (x+3)²+(y-8)²=8².
, пр этом а²=100, b²=36, отсюда с=8, а фокусное расстояние F=2*с=16, радиус окружности R=8. Уравнение окружности радиуса R с центром в произвольной точке A(a,b) записывается как (x−хц)²+(y−yц)²=R²., здесь хц yц - координаты центра. То есть искомое уравнение окружности (x+3)²+(y-8)²=8².
Другие вопросы по теме Алгебра
Популярные вопросы
- Обчисліть масу 4 моль калія оксидуК2О...
2 - Установите соответствие между понятиями и их значением. Понятие...
3 - По поражаемым объектам компьютерные вирусы делятся на: – файловые...
1 - Почему шопен писал полонезы...
3 - по физики контрольная даю 30подчерк классухи идеален, знаю ...
3 - Упражнение 183. Выпишите из упр. 180 три выделен- ных предложения....
2 - Выпишите грамм. основы и подпишите ПГС, СГС или СИС ...
1 - 7 класс английский язык, можно только ответы...
3 - Написать какие профилактические и оперативные меры осуществляет...
2 - У МЕНЯ КОНТРОЛЬНАЯ! длина прямоугольника равна x см, а ширина...
3