1. Алгебра
  2. Составить уравнение касательной

Составить уравнение касательной и нормали к параболе в точке x0=m
y=nx^2+(n-1)x+m

m=3
n=4

daniar16 daniar16    2   15.12.2019 22:01    0

Ответы
малака малака  10.10.2020 20:51

Подставим в уравнение параболы значения параметров:

y=4x^2+(4-1)x+3\\y=4x^2+3x+3

Найдём значение функции в точке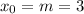 x_0=m=3:

f(x_0)=4 \cdot 3^2+3 \cdot 3+3=48

Найдём производную в точке x₀:

f'(x)=8x+3\\f'(x_0)=8 \cdot 3+3=27

Уравнение касательной имеет вид:

y=f'(x_0)(x-x_0)+f(x_0)\\y=27(x-3)+48=27x-81+48=27x-33

Уравнение нормали имеет вид:

y=-\dfrac{1}{f'(x_0)}(x-x_0)+f(x_0)\\y=-\dfrac{1}{27}(x-3)+48

ответ.

Касательная:

y=27x-33

Нормаль:

y=-\dfrac{1}{27}(x-3)+48


Составить уравнение касательной и нормали к параболе в точке x0=m y=nx^2+(n-1)x+m m=3 n=4
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
эля821 эля821  18.08.2019 13:50
При каком значении p уравнение 2x²-6x+p=0...
danmirlav danmirlav  18.08.2019 13:50
Кстандартному виду многочлен: −13s(44)·t(31)·u(9)·2s(31)·u(17)+44s(10)·t(13)·u(7)·s(5)·t(6)−11s(7)·u(3)·3s(8)·t(19)·u(4)= p/s.числа в скобках-это степени...
Флаксария Флаксария  18.08.2019 13:50
Многочлен к стандрартному виду 1)х*ух+н во 2 степени х 2)6в в 7 степени -4в в 7 степини +8 в в 7 степени -5...
Начинайко Начинайко  18.08.2019 13:50
Впрямоугольном треугольнике abc из вершины прямого угла c проведена высота ch.чему равен bh если ac=6 см,ah=4 см...
оля2036 оля2036  18.08.2019 13:50
Решить неравенство 6в степени х больше либо равно одной тридцатьшесгтой...
245667 245667  08.12.2020 22:57
В) сколько процентов составляет 70 м от 1 км.​...
oksanayarockay oksanayarockay  08.12.2020 22:57
Чи можуть вертикальні кути дорівнювати 21° і 39°​...
ева518 ева518  08.12.2020 22:57
Қакайсысын билесинжер тез жибере салындаршы...
ludmilacernakov ludmilacernakov  08.12.2020 22:57
Вероятность того,что лампочка бракованная 0,03.Покупатель случайно выбирает упаковку с двумя такими лампочками.Найдите вероятность того,что обе лампочки в пачке окажутся исправными....
nikitos7200 nikitos7200  08.12.2020 22:58
На одном чертеже постройте графики функций у = – 2х; у = х + 3; у = – 3....

Популярные вопросы