Составить линейное однородное дифференциальное уравнение, зная характеристики уравнения лямбда в третьей степени = 0

Ответы

АлинаSwons 07.09.2020 00:00

Да тут думать особо нечего.

Характеристическое уравнение получается как следствие из однородного дифференциального уравнения n-го порядка.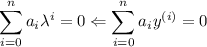 $\displaystyle \sum_{i=0}^{n}a_i \lambda^i=0 \Leftarrow \sum_{i=0}^{n}a_iy^{(i)}=0$

В данном случае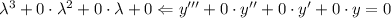 $\lambda ^3+0\cdot \lambda ^2+0\cdot \lambda + 0 \Leftarrow y'''+0\cdot y''+0\cdot y'+0\cdot y=0$

А в обычном виде без нулей это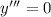 y'''=0

У характеристического уравнения один корень кратности 3, поэтому решение этого уравнения выглядит так:

$y=e^{0\cdot x}(C_1+C_2x+C_3x^2) = C_1+C_2x+C_3x^2, \ \forall C_1,C_2,C_3 \in \mathbb{R}$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

Ychi1ka 05.04.2021 18:37

Три числа складають геометричну прогресію. Сума цих чисел 126, а їх добуток 13824. Знайти ці числа...

GoldenKookieBunny 05.04.2021 18:37

.Использя график функции найдите множество значений переменной при которых принимает неположительные значения функция...

KoCmiK11 05.04.2021 18:37

побудуйте графік функції y=-2x+5. Визначте: 1) Значення функції, якщо значення аргументу дорівнює 2. 2) Значення аргументу, при якому значення функції дорівнює -1...

marina27081981 05.04.2021 18:37

Упростить выражение: ( ) А) -3х(2-х) +(3х+1)(х-2 Б) (х+3)2 –(х-4)(х+4) ПОЛНЫЙ ОТВЕТ ...

Ymnichkaaaaaa 05.04.2021 18:37

Найдите значение выражения 6)x + 3х+при х =хx - 31,5; 2; 3;2сначало сделайте 6 ♡♡♡...

dendiololosh 05.04.2021 18:37

решить подстановки {6x-4y=3 {- 3x+2y=4...

konoplynkoyanoka 05.04.2021 18:36

Решите хотя бы одно задание из предложенных...

guara3 17.08.2019 12:55

Решите систему уравнения а+в=7 5а-3в=11...

Uliana44441 17.08.2019 14:10

Тригометричних функцій кута альфа, якщо відомо, що cosальфа=-0,23 i пи...

alenadasha80 17.08.2019 12:29

Укажіть первісну функції f(x)=cos x графік якої проходить через точку a(π/2 ; 6)...

Составить линейное однородное дифференциальное уравнение, зная характеристики уравнения лямбда в третьей степени = 0

Популярные вопросы