Составь математическую модель по словесной: сумма катетов прямоугольного треугольника равна 31 ,
а его гипотенуза равна 25 . Вычисли площадь треугольника.
Выбери подходящую математическую модель, обозначив длину одного катета как , а другого — :
мм
мм
x мм y мм
Другие вопросы по теме Алгебра
Популярные вопросы
- Дома подбери и запиши слова-названия предметов: 4 слова с окончанием -а, 2 слова...
1 - Решить уравнение. (x-5)^2\x^2=-7x/x+2)^3=0...
3 - песнь о роланде . кратко опишите эту поэму....
3 - Воду v=10 л при температуре=90 градусов смешали с 1 кг воды при 10 градусах....
1 - Двоичное число 11100100001 равно восьмеричному числу а)3441; в)7142; с)6461;...
2 - Почему для измерения величины с учётом её абсолютной погрешности необходимо найти...
2 - Вчем состоит главная роль информации для живой природы? примеры органов чувств...
3 - 5класс. примеры объектов на территории вашего района (республика коми), являющихся...
2 - Какая сцена в пьесе ромео и джульетта считается завязкой а какая развязкой?...
1 - 2дм больше или меньше 1м и каким знаком пишется?...
3
5.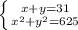
Объяснение:
Сумма катетов равна 31, значит катет x + катет y = 31.
Гипотенуза в прямоугольном треугольнике вычисляется по формуле:
Формула площади прямоугольного треугольника:
x и y нам не известны, но мы можем найти их, решив найденную систему уравнений:
Один из катетов равен 7, другой - 24. Подставляем в формулу площади: