Сократите дробь:
а) 5-√5/√10-√2;
б) b-4/√b-2.
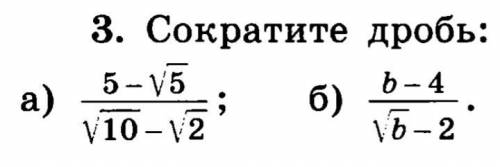
Другие вопросы по теме Алгебра
Популярные вопросы
- Аквариумная рыбка 4 буквы, первая Г...
1 - замените согласованные определения несогласованными:птичьи крики,светловолосая...
2 - 1. «Тебіндеу» сөзіне анықтама беріңдер. 2. Оқулық мәтінін пайдаланып,...
3 - 10 см³ перевести в м³, 30 см³ перевести в м³...
3 - Реши столбиком 714:34 688:16 7644:78 6348:69 с проверкой...
1 - Подготовьте тезисный план объеденив сообщение учеников...
3 - Сторона параллелограмма равна 4 и 7 см, а угол между ними 30°.Найти...
3 - ответьте на 4 вопроса!?? 1) какие приёмы изображения людей на рисунках...
1 - С какими трудностями столкнулась Индия в XVIII в? Какие проблемы пришлось...
3 - ЕЖазылым 2-тапсырма. Суретке қара. Сөйлемді толықтырып жаз.1.Бұл —...
1
Смотри
а) Для начала сократим дробь (5-√5)/(√10-√2):
Чтобы избавиться от знаменателей с радикалами, умножим их на сопряженные значения, то есть (√10+√2) и (√10+√2). Получим:
((5-√5)(√10+√2))/((√10-√2)(√10+√2)).
Произведем умножение числителя:
(5√10+5√2-√50-√10)/(√10^2-√2^2).
Упростим знаменатель и числитель:
(5√10+5√2-√50-√10)/(10-2).
Сгруппируем подобные слагаемые:
(4√10+5√2-√50)/(8).
Дробь нельзя сократить, так как числитель не имеет общих делителей с знаменателем.
Итак, сокращенная дробь равна (4√10+5√2-√50)/8.
б) Теперь посмотрим на вторую дробь (b-4)/(√b-2):
Мы не можем сократить эту дробь, так как числитель и знаменатель содержат переменную и не имеют общих делителей.
То есть, сократить данную дробь не представляется возможным.
В итоге, ответ на первую задачу равен (4√10+5√2-√50)/8, а на вторую задачу дробь не может быть сокращена.