Сократите дробь 1) 24a^6b^4/16a^3b^7 2) 15x-10xy/5xy 3) 25-a^2/a^2-10a+25

Ответы

лера2154 04.10.2020 00:04

Сократить дробь - это значит разделить числитель и знаменатель дроби на одно и то же выражение так, чтобы сделать дробь несократимой.

Нужно знать тождество (a - b)² = (b - a)².

См. решение на рисунке

Сократите дробь 1) 24a^6b^4/16a^3b^7 2) 15x-10xy/5xy 3) 25-a^2/a^2-10a+25

ПОКАЗАТЬ ОТВЕТЫ

Kek1928 04.10.2020 00:04

Решение в разделе "Пошаговое объяснение".

Объяснение:

1) Сократим числа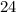 (в числителе) и 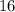(в знаменателе) на 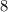. Далее сократим 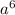a^6 (в числителе) и 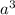a^3 (в знаменателе) на 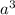a^3 . В конце сократим 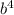b^4 (в числителе) и 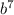b^7 (в знаменателе) на 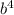b^4 . В итоге получаем:

$\dfrac{24a^6b^4}{16a^3b^7}=\dfrac{3a^6b^4}{2a^3b^7}=\dfrac{3a^3}{2b^3}$

2) Вынесем в числителе за скобку общий множитель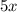 , а затем сократим 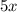и в числителе, и в знаменателе на :

$\dfrac{15x-10xy}{5xy}=\dfrac{5x\cdot(3-2y)}{5xy}=\dfrac{3-2y}{y}$

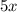3) В числителе представим число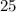 в виде 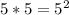5*5=5^2 . По такой записи сразу понятно, что это формула сокращённого умножения (разность квадратов: 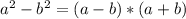a^2-b^2=(a-b)*(a+b) ). Раскладываем эту запись.

В знаменателе тоже скрывается формула сокращённого умножения (квадрат разности: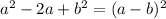 a^2-2a+b^2=(a-b)^2 ).

Далее сокращаем разложенные на множители формулы.

Но для этого нужно в числителе в 1 скобке поменять местам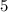и и 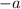и соответственно их знаки. Для этого мы выносим за скобку минус, а в скобке меняем местами числа и их знаки.