1. Алгебра
  2. Снеравенством 2log^2 5 (x^2)

Снеравенством 2log^2 5 (x^2) + 5log 5 (25x) - 8 > = 0

maina342 maina342    2   30.03.2019 08:30    1

Ответы
Reshauvce Reshauvce  27.05.2020 16:12

2\log^2_5 (x^2) + 5\log_5 (25x) - 8 = 0\\ 8\log^2_5 (x) + 5(\log_5 25+\log_5 x) - 8 = 0\\ 8\log^2_5 (x) + 5(2+\log_5 x) - 8 = 0\\ 8\log^2_5 (x) + 10+\log_5 x - 8 = 0\\ 8\log^2_5 (x) +\log_5 x + 2 = 0\\

для наглядности делаем замену

t=\log_5 (x)\\ 8t^2 +5t + 2 = 0

действительных корней неравенство не имеет, т.е. точек пересечения с осбю х нет, это уравнение параболы на ОДЗ логарифма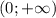 (0; +\infty), при всех значениях х из ОДЗ неравенство истинно

 

----------------------------------------

возможно в задании опечатка.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Танюня123125443 Танюня123125443  07.10.2019 10:20
Чтобы выложить полу ванной комнате, потребуется 180,маленьких квадратных плиток или 80 больших. сторона большой плитки на 5 см больше, чем сторона маленькой. какова площадь...
Стары Стары  07.10.2019 10:10
Найдите сумму всех натуральных чисел a, для которых выполняется равенство нок(a: 266)=266...
lisasmirnova1 lisasmirnova1  07.10.2019 10:10
F(x)=x^3-3x^2+5 1. )для функции y=f(x) найдите: 2область определения; 3точки пересечения с осью ох, с осью оу; 4производную; 5стационарные точки; 6промежутки монотонности;...
Xanuzbek Xanuzbek  07.10.2019 10:10
Разложите квадратный трехчлен на множители: -2x в квадрате +x-3...
nastia6982 nastia6982  07.10.2019 10:10
На одном вестраке нужно обработать 90 деталей, а на другом 100 деталей, при этом на первом верстаке обрабатывется на 5 деталей в час больше, чем на другом. сколько деталей...
Top1lel Top1lel  07.10.2019 10:10
7класс можно решение заранее. выраженях^12×(х^20: х^3)х^22×(х^18×х^21)​...
Anara2017 Anara2017  07.10.2019 10:10
F(x)=x^3-3x^2+5 1. для функции y=f(x) найдите: 1)область определения; 2)точки пересечения с осью ох, с осью оу; 3)производную; 4)стационарные точки; 5)промежутки монотонности;...
fifi17 fifi17  18.09.2021 17:00
9 целый 13/9 - 8 целых 5/5...
рыжик59 рыжик59  18.09.2021 17:04
Выразите J из формулы H=J/D...
Nyashka12 Nyashka12  18.09.2021 17:06
Знайдіть значення а при якому значення виразів 2а-3 і 3-7а дорівнюють один одному...

Популярные вопросы