Скоротіть дріб: 3x²-5x-2

2-4

Знайти площу прямокутного трикутника, якщо один з його катетів на 14 см менший від другого, а гіпотенуза дорівнює 34 см.

с решением и дискриминантом

Ответы

losangelina23 30.05.2023 10:54

${x}^{2} + 7x + n = 0 \\ x_{1} = 4$

По теореме Виета:

${x}^{2} + bx + c = 0\\ x_{1} + x_{2} = - b\\ x_{1} x_{2} = c$

$x_{1} + x_{2} = - 7 \\ x_{2} = - 7 - x_{1} = - 7 - 4 = - 11\\ x_{1} x_{2} =n = 4 \times ( - 11) = - 44$

ответ: х = - 11 ; n = - 44

$3 {x}^{2} - 5x - 2 = 0 \\ a = 3 \\ b = - 5 \\ c = - 2 \\ D = {b}^{2} - 4ac = ( - 5) {}^{2} - 4 \times 3 \times ( - 2) = 25 + 24 = 49 \\ x_{1} = \frac{5 - 7}{2 \times 3} = - \frac{2}{6} = - \frac{1}{3} \\ x_{2} = \frac{5 + 7}{2 \times 3} = \frac{12}{6} = 2 \\ {ax}^{2} + bx + c = a(x - x_{1})(x - x_{2}) \\ 3 {x}^{2} - 5x - 2 = 3(x + \frac{1}{3} )(x - 2)$

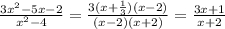
$\frac{3 {x}^{2} - 5x - 2 }{ {x}^{2} - 4 } = \frac{3(x + \frac{1}{3} )(x - 2)}{(x - 2)(x + 2)} = \frac{3x + 1}{ x+ 2}$

34 см - гипотенуза

х - 14 см - один катет

х - другой катет

По теореме Пифагора:

$(x - 14) {}^{2} + {x}^{2} = 34 {}^{2} \\ {x}^{2} - 28x + 196 + {x}^{2} - 1156 = 0 \\ 2 {x}^{2} - 28x - 960 = 0 \\ {x}^{2} - 14x - 480 = 0 \\ a = 1 \\ b = - 14\\ c = - 480 \\ D = {b}^{2} - 4ac = ( - 14) {}^{2} - 4 \times 1 \times ( - 480) = \\ = 196 + 1920 = 2116 \: \: ( \sqrt{D} = 46) \\ x_{1} = \frac{14 - 46}{2} = - \frac{32}{2} = - 16\\ x_{2} = \frac{14 + 46}{2} = \frac{60}{2} = 30$