Сколько существует таких четырёхзначных чисел n, что n^2- n делится на 10000

Ответы

evtpasha2017 22.12.2020 16:30

Одно: n = 9376

Объяснение:

n(n-1) делится на 10^4.

Если одно из чисел (n или n-1) не делится ни на 2, ни на 5, то оно взаимно просто с 10000, и другое число обязано делиться на 10000. Очевидно, таких четырехзначных n, что n или n-1 делится на 10000, нет. Значит, оба числа делятся на 2 или на 5. Два числа вместе делиться на 2 или на 5 не могут, т.к. различаются на 1. Значит, одно из них делится на 2 (не делится на 5), а другое на 5 (не делится на 2).

Пусть, n =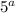 $5^{a}$ * b (a - степень вхождения 5 в разложение n, a≥1). Т.к. n-1 и n взаимно просты, n-1 не делится на 5, поэтому, чтобы n(n-1) делилось на 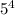$5^{4}$ , нужно чтобы а было ≥ 4.

n ≡ 0 mod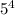 $5^{4}$ .

Аналогично n-1 ≡ 0 mod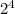 $2^{4}$ (т.к. n не делится на 2) ⇒ n ≡ 1 mod 2^4

Видно, что n = 625 подходит. По кит. т. об остатках, все остальные n получаются прибавлением константы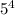 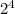$5^{4}$ * $2^{4}$ = 10000, умноженной на целое число. Значит, таких четырехзначных n не существует.

Пусть, n =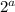 $2^{a}$ * b (a - степень вхождения 2 в разложение n, a≥1). Т.к. n-1 и n взаимно просты, n-1 не делится на 2, поэтому, чтобы n(n-1) делилось на 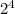$2^{4}$ , нужно чтобы а было ≥ 4.

n ≡ 0 mod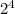 $2^{4}$

Аналогично n-1 ≡ 0 mod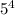 $5^{4}$ (т.к. n не делится на 5) ⇒ n ≡ 1 mod 5^4

Видно, что n = 9376 подходит. По кит. т. об остатках, все остальные n получаются прибавлением константы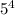 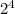$5^{4}$ * $2^{4}$ = 10000, умноженной на целое число. Значит, существует только 1 четырехзначное n = 9376.

Если моё решение Вам отметьте его как лучшее.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра