Сколько существует расставить в ряд 5 шариков белого, красного, синего, жёлтого и зелёного цветов так, чтобы между зелёным и жёлтым шариками стояло не более одного шарика? Есть всего 5 шариков по одному каждого цвета.
Другие вопросы по теме Алгебра
Популярные вопросы
- Придумать либретто к аленькому цветочку...
2 - Даны и соответствующие им сербскохорватские слова: голод – глад, борода –...
1 - Постройте и прочитайте график функции {(-4/(x+1 ),если -5≤x≤-2 y= x2-2,если-2...
1 - Напишите уравнения реакции между водородом и следующими веществами: литием,...
1 - Завтра в школу голова не варит=(( нужно сочинение из 5-6 предложений на тему:...
2 - Вветхом завете сказано и сдвинул он с места два сьолба, на которых утвержден...
3 - 1)определите массу натрия (na), необходимого для получения 4,48 литров (н.у.)...
1 - Найдите корень уравнение log5(2-x)=1...
2 - 1.укажите сущ ,которое образовано путем сложения основ или части основ с...
1 - Для ухода за цветами в доме творчества покупалось 6 упаковок удобрений ежемесячно....
1
Определим общее число расстановок на пяти позициях 5 шариков:
Однако, среди этих расстановок есть недопустимые (то есть те, при которых между зеленым и желтым шариком располагаются два или более шарика). Найдем число недопустимых расстановок.
Найдем число недопустимых размещений зеленого и желтого шарика. Их можно просто перечислить:
1) зеленый на 1-ом месте, желтый на 4-ом месте
2) зеленый на 1-ом месте, желтый на 5-ом месте
3) зеленый на 2-ом месте, желтый на 5-ом месте
4) зеленый на 4-ом месте, желтый на 1-ом месте
5) зеленый на 5-ом месте, желтый на 1-ом месте
6) зеленый на 5-ом месте, желтый на 1-ом месте
В каждом из этих случаев оставшиеся три шарика могут размещаться на свободных местах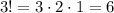
Таким образом, всего имеется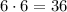 недопустимых расстановок.
недопустимых расстановок.
Значит, допустимых расстановок имеется:
ответ: 84