Сколько решений имеет уравнение
Другие вопросы по теме Алгебра
Популярные вопросы
- І. Назвіть, до яких станів належало українське населення? Пропоную вам розгадати...
2 - Построй график функции y=−2x2+4x Чтобы построить график, определи: 1) направление...
2 - Раскройте скобки используя распределительное свойство умножения 1) 6 * (а -...
3 - Поміркуйте над словами художника: «Мої думки — фарби, мої фарби — наспіви...»....
1 - Выписать 10 междометий ,указать разряд из романа Л.Толстого «Война и мир»...
2 - К концам рычага приложены напрамлени вниз силы 6Н и 4Н. Точка опоры находится...
2 - -2-7у+20=0 көмектесіңіздершіі...
1 - Напишите уравнения реакций, с которых можно осуществить следующие превращения:...
3 - Какие страны стали постоянными членами Совета Безопасности ООН? СССР, США, Бразилия,...
3 - Написать сообщение Место России и Башкортостана в мире за это...
2
x^4+x^2-2=0
Это биквадратное уравнение, нужно произвести замену x^2 на t. Итак, t=x^2
t^2+t-2=0
t=-2
t=1
x^2=-2
x^2=1
x=-1
x=1
ответ: уравнение имеет 2 корня, (-1;1).
Сделаем замену: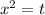 . Тогда:
. Тогда:
Возвращаемся к замене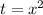 :
:
ответ: уравнение имеет два корня.