1. Алгебра
  2. Скласти квадратне рівняння,

Скласти квадратне рівняння, корені якого дорівнюють:
а) x1=-4; x2=1
б) х1=√2; х2=-3√3

заразарема заразарема    2   26.04.2022 23:59    1

Ответы
almaziksky311 almaziksky311  27.04.2022 01:00

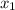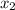Можно воспользоваться обратной теоремой Виета. Если мы знаем корни квадратного уравнения  x_1  и  x_2  , то в квадратном уравнении  

x^2+px+q=0   коэффициенты   q=x_1\cdot x_2\ ,\ \ p=-(x_1+x_2)  .

a)\ \ x_1=-4\ ,\ \ x_2=1\ \ \Rightarrow \ \ p=-(-4+1)=3\ ,\ \ q=-4\cdot 1=-4underline{\ x^2+3x-4=0\ }b)\ \ x_1=\sqrt2\ ,\ \ x_2=-3\sqrt3\ \ \Rightarrow \ \ p=-(\sqrt2-3\sqrt3)=-\sqrt2+3\sqrt3\ ,q=\sqrt2\cdot (-3\sqrt3)=-3\sqrt6underline{\ x^2+(3\sqrt3-\sqrt2)\, x-3\sqrt6=0\ }  

ПОКАЗАТЬ ОТВЕТЫ
46hitman46 46hitman46  27.04.2022 01:00

а) х²+3х-4=0

б) х²+(3√3-√2)х-3√6=0

Объяснение:

(х-х₁)*(х-х₂)=0 - уравнение, имеющее корни х₁ и х₂

а) (х-(-4))*(х-1)=0

(х+4)*(х-1)=0

х²-х+4х-4=0

х²+3х-4=0

б) (х-√2)(х-(-3√3))=0

(х-√2)(х+3√3)=0

х²+3√3х-√2х-3√6=0

х²+(3√3-√2)х-3√6=0

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
rodionmihailof rodionmihailof  30.12.2020 09:38
Решение уравнений. Урок 8 Каждое уравнение соедини с двумя подходящими элементами – названием и необходимой заменой.​...
15082 15082  30.12.2020 09:46
Найдите промежутки возрастания функции 5(8) =5+41 , 1) (-2). [0;2)2) (-2; 2)3) (-е;0],[2;+)4) (-2; 0],[2;+)Найдитеточки минимума функции 1()=-97-9x-5.1) -3.2) 93) 34) - 3; 33Найдите...
Fatimochkaananas Fatimochkaananas  25.08.2019 06:40
При каких значениях x трехчлена -2x^2 + 3x -1 равна нулю? а) 1; 1/2 б) -1; - 1/2; в) 2; 1; г) -1; 2. решите...
Nastya060104sataeva Nastya060104sataeva  25.08.2019 06:40
1укажите промежуток на котором функция f(x)=1/3*x^3-9/2*x^2+8x-3 убывает 2.найдите точку максимума функции f(x)= -3x^2+12x-5 3 cколько критических точек имеет функция f(x)=2x^3+x^2-2x+5...
Dianochka2346587 Dianochka2346587  25.08.2019 06:50
Представь квадрат двучлена в виде многочлена (78−14t7)2...
vamagic2001 vamagic2001  25.08.2019 06:50
Решить уравнения: а) (3х-5)√3х-1=5(3х-5) б) √х²-6х+9+√х²-4х+4=7...
Дарья22031 Дарья22031  25.08.2019 06:50
Впишите вместо многоточия какое-либо число так, чтобы полученное неравенство было верно при любых значениях а и b...
Udjfjwojzksnsnsnslkm Udjfjwojzksnsnsnslkm  25.08.2019 06:50
Разложи на множители (u+21v)2−(21u+v)2...
colaboyy7704ox6ktx colaboyy7704ox6ktx  25.08.2019 06:50
Втреугольнике авс угол с=90 градусов, св=5 см, tgb= 2 найти: ав...
пмпсасрчвчврсв пмпсасрчвчврсв  25.08.2019 06:50
Найдите площадь прямоугольного треугольника , если его катет и гипотенуза равна соответственно 12и 13...

Популярные вопросы