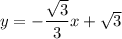Складіть рівняння прямої , зображеної на рисунку
Другие вопросы по теме Алгебра
Популярные вопросы
- Буду ! по графику зависимости давления жидкости от глубины погружения...
1 - Лапицкая 3класс 2часть стр15 4как...
3 - Точки m и k равноудаленны от каждой вершины прямоугольника abcd. расстояние...
1 - 25 ! центрально-східна європа: вибір між демократією та авторитаризмом...
1 - Знайдіть площу паралелограма abcd, якщо ab=a, ac=d, кут bac=alpha...
3 - Охарактеризовать любое получение металла...
2 - Надо написать тест на на тему my working day рабочий день сварщика заранее...
3 - Можете из рассказа чехова смерть чиновника заменить прямую речь,чтобы...
3 - Произведение: герой нашего времени. характеристика контрабандистов: старуха...
1 - Число род и падеж всех прилагательных...
2
Функція є лінійною, тому її рівняння має вид: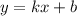 .
.
Візьмемо точки, зображені на графіку.
Однак для рівняння нам не вистачає ще одного значення -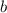
Для його знаходження ми використаємо прямокутний трикутник з гострим кутом 30° (180° - 150° = 30°). Коефіцієнт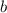 - то є перетин з віссю
- то є перетин з віссю 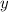
З трикутника: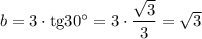
Тепер підставимо всі знайденні вище коефіцієнти в формулу лінійної функції і знайдемо значення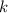 :
:
Отже, рівняння прямої має вид: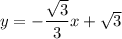 .
.
Відповідь: