1. Алгебра
  2. Складіть рівняння дотічної до

Складіть рівняння дотічної до графіка функції f(x)=x^#-5x в точці x0=2

Zagyart Zagyart    3   01.05.2020 02:45    1

Ответы
Znatokkekgg Znatokkekgg  04.08.2020 13:18

Знайдемо значення функції в точці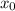 x_0:

f(x_0)=f(2)=2^3-5 \cdot 2=8-10=-2

Знайдемо похідну:

f'(x)=3x^2-5

Знайдемо значення похідної в точці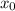 x_0:

f'(x_0)=f'(2)=3 \cdot 2^2-5=7

Загальне рівняння дотичної має вигляд:

y=f'(x)(x-x_0)+f(x_0)

Підставимо відомі значення:

y=7(x-2)-2=7x-14-2=7x-16.

Відповідь: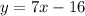 y=7x-16.


Складіть рівняння дотічної до графіка функції f(x)=x^#-5x в точці x0=2
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ппво ппво  21.11.2019 17:31
Выберите из предложенных зависимостей между переменными у и х линейные функции,запишите их ы виде у=кх+b и определите коэффициенты к и ba)у=-х+5; б)у=4-3хв)у=12хг)у=х: 2д)у=7:...
Nika31303 Nika31303  21.11.2019 17:31
Выполните действия: 6d/d-e - 6e/d+e...
Zhuldyz2005 Zhuldyz2005  21.11.2019 17:31
(20 ) 1. найти значение функции () = 15 − 10, соответствующее значению аргумента: а) = 15; б) = −20; в) = 6,05; г) = −9,8....
020910 020910  21.11.2019 17:33
Найти точку минимума функции y=(x^2+6x+9)*e^2-x​...
Artemmundryl Artemmundryl  21.11.2019 15:35
Решить! можно без решения только ответ! заранее) ​...
72737 72737  21.11.2019 15:36
Пример линейной функции график которой пересекает ось у в той же точке что и график функции у=x+11. у=-9х +6...
denthegamerp01iih denthegamerp01iih  21.11.2019 15:38
Найдите значения суммы и произведения корней уравнения: х^2-7х+12=0; -х^2+3,5х-2=0; 5х^2+9х-18=0​...
SSEMAA SSEMAA  21.11.2019 15:39
Пстройте график л инейных функций и выясните их взаимное расположение y=-x+1,5 и y=2x -3​...
sabina1705 sabina1705  16.12.2020 18:56
4х - 7y = 30,4х – бу = 90;...
gunggunggung gunggunggung  16.12.2020 18:56
Плоскость a параллельна основанию AD трапеции ABCD и пересекает ее боковые стороны в точках M и N . Если AD= 17 см, BC= 9 см,то найдите длину отрезка можете...

Популярные вопросы