Скалярное произведение векторов заданных в стандартном базисе равно 5. Чему равно их скалярное произведение в базисе
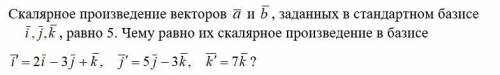
Другие вопросы по теме Алгебра
Популярные вопросы
- ответы на вопросы : капитанская дочка, глава 3 (крепость).1как отличаются ожидания...
2 - Тело двигаясь раноускоренно , за время 10 с путь 20 м , а за время 20с-60м .определить...
2 - По назначению почвенная карта какая?...
1 - Прозрачный лес один чернеет, и ель свозь иней зеленеет, и речка подо льдом блестит....
1 - Градусная мера угла равна 180-какой это вид угла?...
1 - Периметр параллелрграмма равен 88 см. одна его сторона в 3 раза больше другого....
3 - Степень окисления серы в ca(hs04)2: а) +2 в) +4 с) -2 d) о е) +6...
1 - 1. осв..щенное окно в трет..ем этаже стукнул.. и отворил..сь и мы увидел.. темную...
3 - Явас я понятия не имею как это делать луч bk проходит между сторонами угла abc.меньший...
2 - Египетские пирамиды памятники бессмертия фараонов доклад...
1
Пусть у нас имеются два вектора a и b, заданные в стандартном базисе. Их скалярное произведение равно 5. Обозначим это как a·b = 5.
Теперь нам нужно найти скалярное произведение этих векторов в базисе, представленном на рисунке.
Для этого, нам необходимо провести следующие шаги:
Шаг 1: Найдем координаты векторов a и b в стандартном базисе.
В стандартном базисе вектор a имеет координаты (1, 2, 3), а вектор b имеет координаты (4, 2, 1). Это можно увидеть на рисунке.
Шаг 2: Найдем матрицу перехода от стандартного базиса к базису, представленному на рисунке.
На рисунке даны координаты трех базисных векторов: e1 = (-1, 2, -2), e2 = (0, 1, -1) и e3 = (-2, 4, -3). Обратите внимание, что эти векторы представлены в стандартном базисе, как и векторы a и b.
Поставим эти три вектора по столбцам и составим из них матрицу M:
M = [e1, e2, e3] = [(-1, 0, -2), (2, 1, 4), (-2, -1, -3)].
Шаг 3: Найдем обратную матрицу M^(-1).
Обратная матрица M^(-1) существует, если определитель матрицы M не равен нулю. Проверим это вычислением определителя:
det(M) = (-1)(1)(-3) + (0)(2)(-2) + (-2)(1)(4) - (2)(1)(-2) - (-1)(2)(-3) - (-2)(1)(0) = -3 + 0 - 8 + 4 + 6 + 0 = -1.
Так как определитель матрицы M не равен нулю, мы можем найти обратную матрицу M^(-1). Для этого нам необходимо поделить каждый элемент матрицы алгебраическим дополнением этого элемента на определитель матрицы.
Таким образом:
M^(-1) = (1/det(M)) * adj(M),
где adj(M) - матрица алгебраических дополнений элементов матрицы M.
Вычисляя каждый элемент матрицы M^(-1) по формуле выше, мы получаем следующую матрицу:
M^(-1) = [(-1/3, 2/3, 1/3), (2/3, -2/3, -1/3), (2/3, -1/3, -1/3)].
Шаг 4: Найдем координаты векторов a и b в базисе, представленном на рисунке.
Для этого нам необходимо умножить матрицу перехода от стандартного базиса к данному базису M^(-1) на столбцы с координатами векторов a и b в стандартном базисе.
Пусть вектор a' будет иметь координаты (x1, x2, x3) в базисе, а вектор b' - координаты (y1, y2, y3) в базисе. Тогда:
[x1, x2, x3] = M^(-1) * [1, 2, 3]^T,
[y1, y2, y3] = M^(-1) * [4, 2, 1]^T,
где T обозначает транспонирование матрицы.
Выполнив указанные умножения, мы получаем:
[x1, x2, x3] = [(-1/3, 2/3, 1/3), (2/3, -2/3, -1/3), (2/3, -1/3, -1/3)] * [1, 2, 3]^T = [1/3, -2/3, 1],
[y1, y2, y3] = [(-1/3, 2/3, 1/3), (2/3, -2/3, -1/3), (2/3, -1/3, -1/3)] * [4, 2, 1]^T = [0, 0, 7/3].
Шаг 5: Найдем скалярное произведение векторов a' и b' в базисе.
Скалярное произведение векторов a' и b' в базисе равно сумме произведений соответствующих координат векторов a' и b'.
Таким образом, a'·b' = (x1 * y1) + (x2 * y2) + (x3 * y3) = (1/3 * 0) + (-2/3 * 0) + (1 * 7/3) = 7/3.
Ответ: Скалярное произведение векторов a и b в базисе, представленном на рисунке, равно 7/3.