Система логарифмических уравнений. Я знаю, что в 1 уравнении вроде как работает формула суммы кубов..

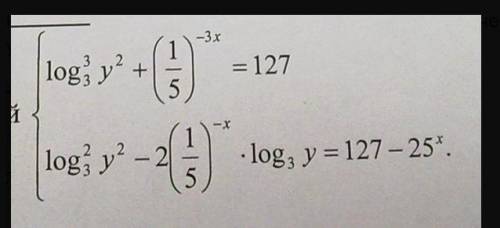
Система логарифмических уравнений. Я знаю, что в 1 уравнении вроде как работает формула суммы кубов.

Ответы

karinapolushin 25.02.2021 21:53

$\displaystyle ODZ: y0$

$\displaystyle\left \{ {{log^3_3y^2+5^{3x}=127} \atop {log^2_3y^2-2*5^x*log_3y=127-5^{2x}}} \right. \\\\\left \{ {{log^3_3y^2+5^{3x}=127} \atop {log^2_3y^2-5^x*log_3y^2+5^{2x}=127}} \right.$

сделаем замену

$\displaystyle log_3y^2=a; 5^x=b$

где b>0

тогда

$\displaystyle \left \{ {{a^2+b^3=127} \atop {a^2-ab+b^2=127}} \right. \\\\\left \{ {{(a+b)(a^2-ab+b^2)=127} \atop {a^2-ab+b^2=127}} \right.$

тогда (a+b)*127=127, значит a+b=1; a=1-b

подставим во второе равенство

$\displaystyle (1-b)^2-(1-b)b+b^2=127\\\\1-2b+b^2-b+b^2+b^2-127=0\\\\3b^2-3b-126=0\\\\3(b^2-b-42)=0\\\\D=1+168=169\\\\b_{1.2}=\frac{1 \pm 13}{2}\\\\b_1=7; a_1=1-7=-6\\\\b_2=-6; a_2=1-(-6)=7$

Рассмотрим II случай а=7 b=-6, но этот случай не подходит по условию

Тогда рассмотрим I случай

a=-6; b=7

$\displaystyle \left \{ {{log_3y^2=-6} \atop {5^x=7}} \right. \\\\\left \{ {{log_3y=-3} \atop {x=log_57}} \right. \\\\\left \{ {{y=3^{-3}} \atop {x=log_57}} \right.$