СИРИУС, НЕ ПОНИМАЮ КАК РЕШАТЬ

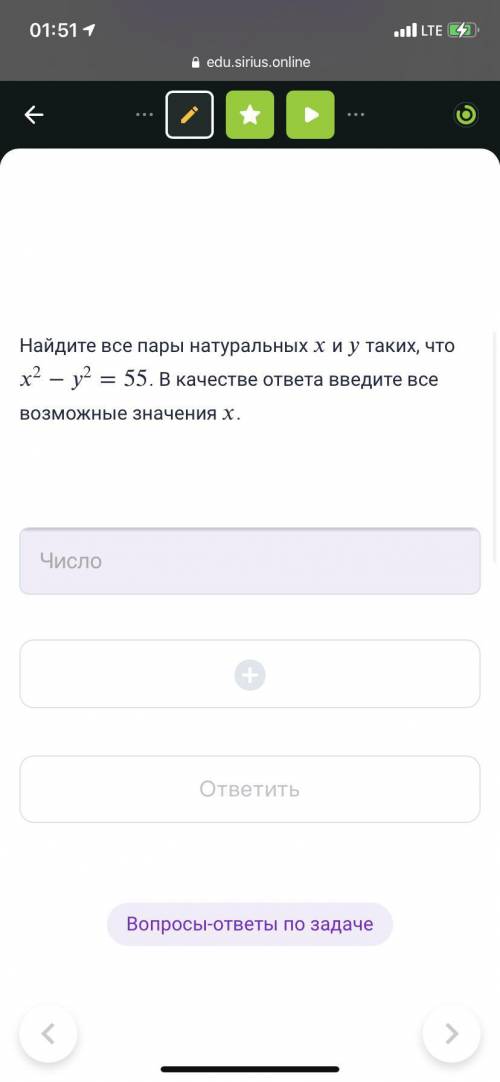
x = 8 или x = 28

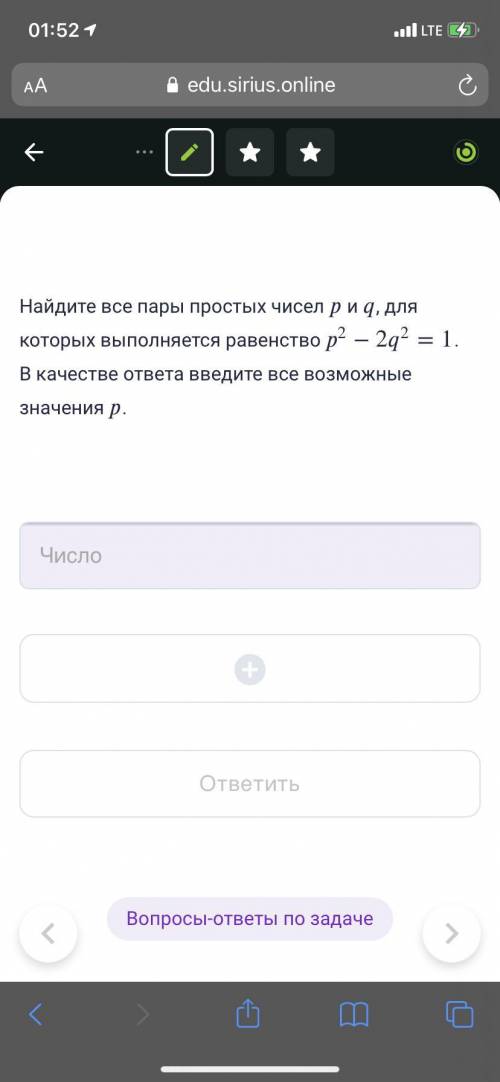
p = 3

Объяснение:

По формуле разности квадратов x²-y²=(x-y)(x+y). Поскольку x и y — натуральные, то они целые, а значит, их сумма и разность тоже целые. Причем сумма натуральных чисел строго положительная, поэтому и разность для выполнения условия задачи должна быть положительной. Учитывая, что 55=5×11=1×55 и других разложений на натуральные множители нет, стало быть, один из множителей выражения x²-y² равен 5, а другой — 11, либо один равен 1, а другой — 55.

(8, 3)

или

Вторая пара решений (8, -3) не удовлетворяет условию, потому что -3 — не натуральное.

(28, 27)

или

Четвертая пара (28, -27) не удовлетворяет условию, потому что -27 — не натуральное.

___________________________________

Немного преобразуем уравнение:

Как и в предыдущей задаче, p+1>0 и p-1>0 (p — простое, 2 — наименьшее простое число).

Правую часть можно представить в виде произведения двух натуральных множителей несколькими : 2q² = 1×2q² = 2×q² = 2q×q

Если один из множителей — 1, а другой — 2q², то только p-1 может быть равно 1 и p=2 (иначе p=0, 0 — не простое). Но тогда p+1=3=2q², q не будет целым.

Если один из множителей — 2, а другой — q², то только p-1 может быть равно 2 и p=3 (иначе p=1, 1 — не простое). Тогда p+1=4=q², q=2 — удовлетворяет условию

Пускай один из множителей — 2q, а другой — q. То есть один из них вдвое больше второго.

2(p-1)=p+1, 2p-2=p+1, p=3, в таком случае 2q²=2×4=8, q²=4, q=2 — удовлетворяет условию

или

p-1=2(p+1), p-1=2p+2, p = -3 — не простое