1. Алгебра
  2. Sin2x=корень из 2 sin(п/2+х)

Sin2x=корень из 2 sin(п/2+х) [-3п; -5п]

Kingston11 Kingston11    3   22.05.2019 07:00    4

Ответы
Bandit009 Bandit009  01.10.2020 06:07

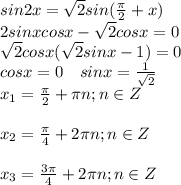
1)sin2x=\sqrt2sin(\frac{\pi}{2}+x)\\2sinxcosx-\sqrt2cosx=0\\\sqrt2cosx(\sqrt2sinx-1)=0\\cosx=0\ \ \ sinx=\frac{1}{\sqrt2}\\x_1=\frac{\pi}{2}+\pi n;n\in Z\\\\x_2=\frac{\pi}{4}+2\pi n;n\in Z\\\\x_3=\frac{3\pi}{4}+2\pi n;n\in Z

2) [-3п;-5п]

Решения ,которые принадлежат данному отрезку(вложение)

-\frac{9\pi}{2};-\frac{15\pi}{4};-\frac{7\pi}{2};-\frac{13\pi}{4}

 

 

 

 

 

 


Sin2x=корень из 2 sin(п/2+х) [-3п; -5п]
ПОКАЗАТЬ ОТВЕТЫ
kira757 kira757  01.10.2020 06:07

sin2x=√2sin(pi/2+х)

2sinxcosx=√2cosx

2sinxcosx-√2cosx=0

cosx(2sinx-√2)=0

 

cosx=0

x=pi/2+pik, k∈Z

 

sinx=√2/2

x=pi/4+2pik, k∈Z;

x=3pi/4+2pik, k∈Z

 

 

 

 

 


Sin2x=корень из 2 sin(п/2+х) [-3п; -5п]
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
6jytu 6jytu  15.01.2021 10:47
Решение текстовых задач с составления дробно-рациональных уравнений. Урок 2 Автобус проехал от остановки до аэропорта 40 км. Через 10 минут опоздавший пассажир выехал за автобусом...
masha6610 masha6610  15.01.2021 10:48
Дано: (an) - арифметическая прогрессияa1 = 15; a2 = 3Найти: a2 + a4...
kdjdn25 kdjdn25  15.01.2021 10:50
Найдите два любых решения а) x²+y=7 б) (x-1)(y+1/5)=0​...
klarkwin klarkwin  14.12.2020 21:58
Алгебра, 7 класс желательно хотя бы 3 номера(​ >...
vika02bel vika02bel  14.12.2020 21:58
5. Розв‘яжіь рівняння б) (2х – 3)(х + 7) = (х – 4)(2х + 3) + 3; в) х2 – 2х + 5 (х нужно!...
Агаисмаил1 Агаисмаил1  14.12.2020 21:59
Cos 5x cos3x-sin 5x sin 3x=cos 8x...
Gbdngggvg Gbdngggvg  16.12.2021 11:14
Площа зафарбованої фігури якщо радіус круга 21 сс ширина прямокутника 5 см а довжина 12 см...
милка328 милка328  16.12.2021 11:14
Дано уравнение 7x2+37x−11=0. Запиши старший коэффициент, второй коэффициент и свободный член. Старший коэффициент . Второй коэффициент . Свободный член ....
Ihalina Ihalina  16.12.2021 11:14
620. Запишите в стандартном виде многочлен: номер 620...
PatiFon4ik PatiFon4ik  16.12.2021 11:16
Раскрой скобки: (−11−d)(m−4)....

Популярные вопросы