Sin2x-2 корня из 3 cos x в квадрате - 4 sinx + 4 корня из 3 cosx = 0
Другие вопросы по теме Алгебра
Популярные вопросы
- Як називаються анонімні угрупування тварин,члени яких є агресивними до нових...
2 - Якими чотирма можна добути CuCl2...
2 - окончание 2) основа 3) согласных 4) Четвертого не мог найти...
1 - Написать рассказ Празднование 1 мая в школе 30-40 слов на казахском (желательно...
2 - В декабре школьники установили 4 кормушки,а в феврале в 5 раз больше.Сколько...
2 - ОТ КОНТРОЛЬНАЯ. 8КЛ. ХИМИЯ. Хлор об ємом 0.224 л (н. у.) повністю прореагував...
3 - Решите плз бан не очень охота получать ...
2 - 12. Даны четыре параллельные прямые, пересекающие стороны угла вточках Ан...
1 - Если тебя кикнуло перед пейдеем а ты отыграл 25 минут за час мне начислится...
3 - Агент фікса з усіх циркачів вподобав тільки. а імпресаріо пандорського б...
3
Помню решал уже эту задачу, она в каком-то сборнике по подготовке к ЕГЭ. Тройка в скобках это корень из 3.
2sinx*cosx - 2(3)cosx(cosx-2) - 4sinx=0
2sinx( cosx-2)-2(3)cosx(cosx-2)=0
cosx=2 2sinx-2(3)cosx=0
нет решений sinx-(3)cosx=0 | делю на cosx
tgx-(3)=0
tgx=(3)
x=n/3+nz ( n- 3.14 т.е. пи)
ответ: х=n/3 + nz
ответ: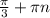 ; n∈Z
; n∈Z