Sin=![\frac{-2\sqrt[2]{6} }{5}](/tpl/images/3779/4599/f9d8f.png) Найти Cos на промежутке (
Найти Cos на промежутке (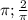 )
)
Другие вопросы по теме Алгебра
Популярные вопросы
- Запишите вставля пропушенные буквы почеркните главные члены в каждом...
3 - Сравните числа 1.arcsin(-1/2) и arccos(-1/2) 2. arccos(-корень3/2) и...
3 - Сочинение нравственные советы древней руси...
3 - Продолжите фразу: загадка человека в том, что он-единство двух а) биологической...
2 - Как читаются эти слова по teacher,doctor,driver,worker,cosmonaut,actor,scientist,gardener,painter,writer,poet...
3 - На ферме 160л молока разлили в 5 бидонов,ёмкостью 20л каждый и в несколько...
3 - Значення фразеологізму жовчю сходити...
3 - Какие события произошли в 1721 год...
3 - За одну минуту марина может присесть 20 раз,а её старший брат в 4 раза...
1 - Используя в качестве темы любой фразеологизм из .124,напиши небольшое...
3
sin²x+cos²x=1 ⇒ cos²x=1-sin²x⇒
Если x ∈ (π/2; π), то косинус во второй четверти отрицательный:
Если x ∈ (π; 3π/2), то косинус в третьей четверти отрицательный: