Sin 18 (с тригонометрии) с подробным описанием решение защитаю если полностью объясните вот это решение sin 36°= cos 54°= cos (18° + 36°); 2 sin18° cos18° = cos18° cos36° – sin18° sin36°; 2 sin18° cos18°= cos18°(1 – 2sin218°) – 2sin218°cos18° 2 sin18° = 1 – 4sin218°, решаем квадратное уравнение и учтем, что sin18° > 0, получим sin18° = .(корень5-1)/4
Другие вопросы по теме Алгебра
Популярные вопросы
- Вычислить удельную теплоемкость цезия при температуре 2 К. Температура...
1 - Скажите английский решить Я вас...
3 - Знайдіть спільне та відмінне в природних умовах Греції й Італії за таким...
3 - с философией! Что означает свобода пред обществом и свобода перед собой?...
1 - Запишите неправильную дробь в виде смешаной дроби 16/3 и решить оьмечу...
3 - Как на Руси называли представителя хана, который следил за порядком и контролировал...
3 - Укажите предложение (ия) в которых есть указательное слово...
3 - Урал охарактеризовать ПОДРОБНО План характеристики: 1.ФГП - границы; -...
1 - Найти периметр и площадь квадрата, сторона которого равна 3,8 см....
2 - Нужно написать краткий проект про знаменитости Ленинского района (список...
3
по формуле приведения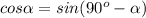
так как 18+36=54, то
т.е.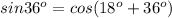 (1)
(1)
по формуле синуса двойного угла(аргумента)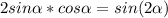
по формуле косинуса суммы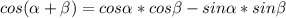 :
:
Подставив (2) и (3) в (1) получим
используя формулы синуса двойного угла (выше упоминалась) и косинуса двойного угла
имеем что
Подставляя (5) в (4), упращая и сокращая обе части равенства на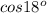
Получили квадратное уравнение относительно sin 18
так как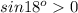 , как синус острого угла (т.е. угла большег 0 градусов и меньшего 90 градусов)
, как синус острого угла (т.е. угла большег 0 градусов и меньшего 90 градусов)
Как-то так*