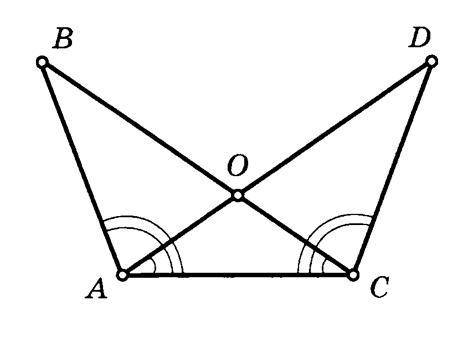
Сформулируйте доказательство равенства треугольников ABC и CDA, изображенных на чертеже. Рассмотрим Δ ABC и Δ CDA. В них(),()

Question

Алгебра: Сформулируйте доказательство равенства треугольников ABC и CDA, изображенных на чертеже. Рассмотрим Δ ABC и Δ CDA. В них(),() ,() . Таким образом, Δ ABC = Δ CDA (), что и требовалось доказать.

Geopolit · Answer

Объяснение:Рассмотрим ΔABС и ΔCDA. В них BAC= DCA как соответствующие суммы равных углов ( BAO+ DAC)=( DCO+ BCA). AC - общая сторона, а DAC= BCA по условию.Таким образом, ΔABC = ΔCDA по 2-му признаку, что и требовалось доказать....

Популярные вопросы