Сформулированы следующие два утверждения: а) уравнение ax - sqrt(x) + 1 = 0 имеет ровно одно решение б) неравенство x^2 - 8ax + 1 < = 0 имеет хотя бы одно решение определить все значения параметра а, при каждом из которых оба утверждения
справедливы

Ответы

Aly6000 23.05.2020 23:54

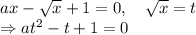а) $ax-\sqrt x+1=0,\quad\sqrt x=t\\\Rightarrow at^2-t+1=0$ .

Это квадратное уравнение имеет один корень, если его дискриминант равен нулю, т.е.

$1-4a=0\Rightarrow a=\frac14$

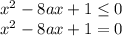
б) $x^2-8ax+1\leq 0\\x^2-8ax+1= 0$

Это квадратное уравнение имеет хотя бы один корень, если дискриминант неотрицателен, т.е.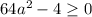 $64a^2-4\geq0$ . Это неравенство справедливо при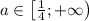 $a\in\left[\frac14;+\infty\right)$

ПОКАЗАТЬ ОТВЕТЫ

КаринаХасанова9 23.05.2020 23:54

а) Рассмотрим уравнение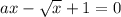 $ax-\sqrt{x}+1=0$ (a=0 подходит тогда х=1)сделаем замену переменных 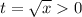$t=\sqrt{x}{0}$ . Получим уравнение

at^2-t+1=0 (здесь $a\neq{0}$ )Данное квадратное уравнение имеет 1 корень, если дискриминант D=0. Однако, если уравнение имеет 2 решения, причем разного знака, то нам подходит только одно положительное. Следовательно, в этом случае исходное уравнение будет иметь тоже 1 корень. Поэтому рассматриваем случай, когда $D\geq{0}$

$D=1-4a\geq{0}$ Тогда $a\leq{\frac{1}{4}}$

Далее пусть меньший корень будет < 0, а больший >0.

Необходимо рассмотреть 3 случая:

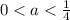
1) $0<a<\frac{1}{4}$

$x_1=\frac{1-\sqrt{D}}{2a}<x_2=\frac{1+\sqrt{d}}{2a}$

x_1<0 Тогда D>1, следовательно a<0. Получаем нет решений.

2) a<0

$x_2=\frac{1+\sqrt{D}}{2a}<x_1=\frac{1-\sqrt{d}}{2a}$

x_2<0 Тогда $\sqrt{D}-1$ всегда выполняется.

x_10 Тогда D>1, следовательно a<0.

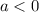
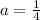
3) $a=\frac{1}{4}$

t=20

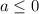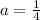
Таким образом $a\leq{0}$ и $a=\frac{1}{4}$

б) неравенство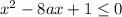 $x^2-8ax+1\leq{0}$ будет иметь хотя бы один решение, если 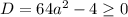$D=64a^2-4\geq{0}$ . Отсюда получаем a из $(-\infty ; -\frac{1}{4}]\cup{[\frac{1}{4};+\infty)}$