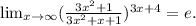,сегодня нужно сдать,а я никак не могу решить ( ) lim x → ∞ (3x2+1/3x2-x+1)^3x+4

Другие вопросы по теме Алгебра
Популярные вопросы
- РЕШИТЕ,УМОЛЯЮ 1. Рассчитайте относительную молекулярную массу (Mr) для следующих...
2 - Твір на тему що ми вивчали по фізиці у 8 класі...
1 - Вероятность того, что студент знает ответ на во в билете на экзамене 0,8....
3 - Прочитать поэму Белгород, написать рассуждение...
3 - балов Напряжение в цепи переменного тока изменяется по закону u = um sinwt....
2 - Решить каждое уравнение и вернуться в колонку 2...
2 - Найдите первообразную для функции F(x)=x-4 , которая равна 2 при x=4....
1 - Составьте уравнения процессов на аноде и катоде, суммарное уравнение и схему...
2 - Insert the necessary word combinations:1. It had been realised for some time...
2 - 1. Дайте определение Лимита кассы. Какой нормативный документ регламентирует...
3
Объяснение:
тяжело записать, но попробую. пишите lim и степень за скобкой как указано. в скобке будет следующее: = (3x^2+1+x-x)/(3x^2-x+1)=(1+ x/(3x^2-x+1)=(1+1/x/(3x^2-x+1) это трехэтажная дробь, =(1+1/(3x^2-x+1)/x степень скобки будет (3x^2-x+1)/x, ставим еще скобку, за ней обратная степень х/(3x^2-x+1), эту домножаем на данную степень 3х+4. теперь убираем предел = е^lim(x*(3x+4))/(3x^2-x+1)=е^lim(3x^2+4x)/(3x^2-x+1)=e^1=e
Объяснение:
Используем свойства второго замечательного предела:
ответ: