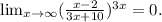,сегодня нужно сдать,а я никак не могу решить ( ) lim x → ∞ (x-2/3x+10)^3x
Другие вопросы по теме Алгебра
Популярные вопросы
- ТЕКСТ ЗАДАНИЯ Перед Вами две иллюстрации к сказке О. Уайльда Соловей и Роза .извини...
1 - Какую роль сыграла погода в день сражения под Прохоровкой?...
3 - 224. При будь-якому п суму з перших членів деякої арифметичної прогресії можна обчислити...
1 - Що вплинуло на рішення Санчо Панси супроводжувати Дон Кіхота? Що незвичного було...
1 - сколько вариантов будет если рассадить 5 человек на 5 мест? Очень ...
3 - Подберите нужное слово в предложении...
1 - Составьте уравнение линии, каждая точка которой равноудалена от точки M0(x0,y0)...
1 - с заданием по химии: 1) Установите число эквивалентности и фактор эквивалентности...
1 - Предложение со словом Маяк мужского женского рода...
2 - Что необходимо сделать для получения из чугуна сталь?(технология)...
1
Объяснение:
ответ: