Сегодня был крайне удивлен когда попытался посчитать пропорцию:
90*0/80 будет 0
Но ведь и ежу понятно что в Х должно быть некое значение отличное от нуля в большую сторону, но оно не решаемо стандартным методом.
Как так?

Ответы

Sanek27rus 20.07.2022 17:09

$\displaystyle \frac{80}{90} = \frac{0}{X}$ .

Заученное без особого понимания "правило пропорции" говорит, что при данном равенстве неизвестная будет равна

$X = \dfrac{90\cdot 0}{80}$ , но это же нуль!

На самом деле "правило пропорции" - ничего более, чем умножение и деление. В самом деле, умножим обе части изначального уравнения на :

$\dfrac{80}{90}\cdot X = 0$ .

Поделим на коэффициент перед неизвестной (или умножим на обратное ему число, что то же самое):

$X = \dfrac{90\cdot 0}{80}$ .

Пришли к результату, которое даёт нам "правило пропорции". Так в чём же проблема? А в самом первом шаге - умножении обеих частей на неизвестную .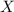

$\dfrac{80}{90}\cdot X = \dfrac{0\cdot X}{X}$ .

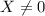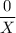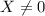Здесь, чтобы сократить неизвестную в правой части уравнения необходимо условие $X\neq 0$ , которое, на самом деле, уже предполагается при постановке задачи. Действительно, выражение $\dfrac{0}{X}$ имеет смысл только при озвученном условии $X\neq 0$ .

Но раз это так, то мы сразу же можем написать значение выражения справа в изначальном уравнении:

$\dfrac{0}{X} = 0,\quad X\neq 0$

И что же мы получим? Получим уравнение на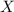 , не зависящее от 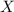, т.е. некоторое равенство, которое должно быть верно для любого значения неизвестной 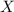. Посмотрим на него:

$\dfrac{80}{90} = 0$ .

Не нужно иметь и семи пядей во лбу, чтобы догадаться, что полученное равенство не верно ни при каком значении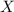 . Отсюда делаем вывод, что изначальное уравнение решений не имеет.

ответ.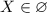 $X\in\varnothing$ .

P.S. Фраза "посчитать пропорцию" вообще особого смысла в себе не имеет - можно с тем же успехом пытаться "считать" равенства или уравнения. Правда для данного случая счёт закончится довольно быстро - у нас всего 1 уравнение.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра