Сделайте хотябы 2 варианта ! 1. решите уравнение: a) (12x+1)(3x– 1)–(6x+2)^2=10; 2. решите уравнение: а ) 9x^3–27x^2=0; в) x^3–4x^2–9x+36=0; б) x^3–64x=0; г) x^3–2x^2=x–2. 3. докажите, что уравнение 12x5+11x3+10x–4=140 не имеет отрицательных корней.

Ответы

Abibkaa 12.06.2020 20:52

$1.~ (12x+1)(3x-1)-(6x+2)^2=10\\ 36x^2-12x+3x-1-(36x^2+24x+4)=10\\ 36x^2-9x-1-36x^2-24x-4=10\\-33x=15\\ x=-\frac{15}{33}=-\frac{5}{11}$

ответ: -5/11.

$a)~9x^3-27x^2=0\\ 9x^2(x-3)=0~~\Leftrightarrow~~ x_1=0;~~ x_2=3$

$b)~ x^3-64x=0\\ x(x^2-64)=0\\ x(x-8)(x+8)=0~~\Leftrightarrow~~~ x_1=0;~x_2=8;~ x_3=-8$

$c)~ x^3-4x^2-9x+36=0\\ x^2(x-4)-9(x-4)=0\\(x-4)(x^2-9)=0\\ (x-4)(x-3)(x+3)=0~~\Leftightarrow~~ x_1=4;~ x_2=3;~ x_3=-3$

$d)~ x^3-2x^2=x-2\\ x^2(x-2)-(x-2)=0\\ (x-2)(x^2-1)=0\\ (x-2)(x-1)(x+1)=0~~\Leftrightarrow~~ x_1=2;~ x_2=1;~x_3=-1$

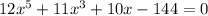
3. 12x^5+11x^3+10x-144=0

Рассмотрим функцию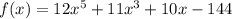 f(x)=12x^5+11x^3+10x-144

Производная функции: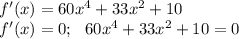 $f'(x)=60x^4+33x^2+10\\ f'(x)=0;~~ 60x^4+33x^2+10=0$

Решим это уравнение как квадратное уравнение относительно x²:

$D=b^2-4ac=33^2-4\cdot60\cdot10=-1311<0$

экстремумов нет, следовательно, функция является монотонно возрастающей, значит, корень вещественный единственный.

По теореме Виета произведение корней равно отношению (-1)ⁿ*c/a, где c- свободный член и a - коэффициент перед старшей степенью х., n - наибольшая степень уравнения

(-1)⁵ * (-144/12) = 12 ⇒ корни положительные

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра