с заданием! Найдите площадь фигуры по рисунку:
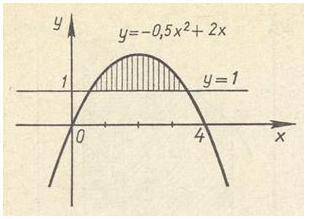
Другие вопросы по теме Алгебра
Популярные вопросы
- Кто обрабатывал народные сказки, кроме а.толстого и м. булатова? (если...
1 - Найди и выпиши лишнего героя вадик котенок володя родители...
3 - №1 у+4х=12, 2х-3у=-22(решите систему уравнений подстановки ) № 2 при какаих...
2 - 1.заполните пропуски в предложении. if he … smarter, he … so. -were, wouldn’t...
1 - Положение дворянства при елизавете петровне...
2 - Запиши строфу стихотворения. выдели граматические основы этого предложения,...
3 - Аминоуксусную кислоту можно получить в одну стадию из кислоты: 1)уксусной.2)хлоруксусной.3)пропионовой.4)2-хлорпропионовой...
3 - По мере удаления вверх от поверхности земли температура воздуха изменялась...
1 - Указать страны снг,не имеющие границы с россией: a)украина в)киргизия...
1 - Какие формы высшей нервной деятельности характерны для животных? ∞условное...
1
Точки пересечения: