с векторами
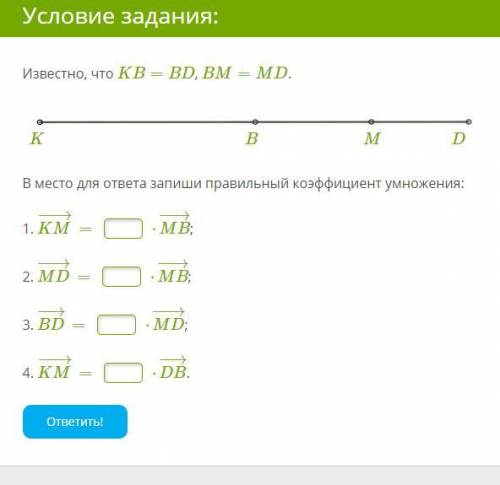
Известно, что KB=BD, BM=MD. K B M D В
Другие вопросы по теме Алгебра
Популярные вопросы
- Вкаком предложении знаки препинание расставлены неправельно? 1)спой светик,не...
3 - Протон движется в однородном магнитном поле с индукцией 5мтл со скоростью 10000...
2 - Найди высоту призмы,объем которой равен 74 см(куб),а в основу входит прямоугольник(площадь...
3 - Напишите уравнения всех возможный реакций между следующими веществами: нитрат...
2 - Нужно написать сочинение рассуждение максимум 7 предложений на тему : что бы лучше...
3 - Какие из дробей нельзя перевести в десятичную дробь: 6/30; 72/112; 7/30; 48/108?...
1 - Народні прекмети в яких ужиаваються прислівники з різним ступенем вияву ознаки...
1 - For questions 1-7, decide which of the following is said about each type. write...
3 - Презентация о необычных фактах стран северной европы...
1 - Вкаком предложении подлежащее выражено инфинитивом? а) наша — дойти до города...
3
Из условия задачи нам дано, что KB=BD и BM=MD. Обозначим векторы следующим образом:
- Вектор KB обозначим как вектор а.
- Вектор BD обозначим как вектор b.
- Вектор BM обозначим как вектор c.
- Вектор MD обозначим как вектор d.
Теперь мы можем использовать данные, чтобы выразить эти векторы. Для этого сначала заметим, что BDM является треугольником.
Треугольник BDM:
Из условия BDM=BDM (следующее постулат) мы знаем, что вектор BD + вектор DM = вектор BM.
b + d = c (уравнение 1)
Теперь мы можем использовать информацию, которую нам дали о KB=BD, чтобы связать векторы а и b.
Из условия KB=BD мы знаем, что вектор KB + вектор BD = вектор 0 (нулевой вектор, поскольку сумма двух векторов равна нулевому вектору).
a + b = 0 (уравнение 2)
Для удобства решим уравнение 2 относительно вектора b:
b = -a
Теперь мы можем заменить b в уравнении 1:
-a + d = c (уравнение 3)
Теперь у нас есть система уравнений:
-a + d = c (уравнение 3)
a + b = 0 (уравнение 2)
Из уравнения 2:
a = -b
Подставим a = -b в уравнение 3:
-(-b) + d = c
b + d = c
Таким образом, мы получаем, что векторы b и d суммируются, чтобы получить вектор c.
Итак, ответ на данный вопрос: вектор c равен сумме векторов b и d. Вектора, данные на диаграмме, тем самым, удовлетворяют уравнению c = b + d.