с уравнениями
y' '+2 y'+5 y=−2sin x
y"-3y=(4x+1)e^2x

Відповідь:

Пояснення:

1.

Cоставляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:

r^2 +2 r + 5 = 0

D=2^2 - 4·1·5=-16

Корни характеристического уравнения: (комплексные корни):

r1 = -1 + 2i

r2 = -1 - 2i

Общее решение однородного уравнения имеет вид:

y- = C1 e^(-x) cos(2x) + C2 e^(-x) cos(2x) , Ci ∈ R

Рассмотрим правую часть:

f(x) = -2*sin(x)

Здесь P(x) = 0, Q(x) = -2, α = 0, β = 1.

Следовательно, число α + βi = i не является корнем характеристического уравнения.

Уравнение имеет частное решение вида:

y· = Acos(x) + Bsin(x)

Вычисляем производные:

y' = -A·sin(x)+B·cos(x)

y'' = -(A·cos(x)+B·sin(x))

которые подставляем в исходное дифференциальное уравнение:

y'' + 2y' + 5y = (-(A·cos(x)+B·sin(x))) + 2(-A·sin(x)+B·cos(x)) + 5(Acos(x) + Bsin(x)) = -2·sin(x)

или

-2·A·sin(x)+4·A·cos(x)+4·B·sin(x)+2·B·cos(x) = -2·sin(x)

Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:

1: -2A + 4B = -2

1: 4A + 2B = 0

Решая ее, находим:

A = 1/5;B = -2/5;

Частное решение имеет вид:

y·=1/5cos(x) -2/5sin(x)

Таким образом, общее решение дифференциального уравнения имеет вид:

y = y- +y. = y- = C1 e^(-x) cos(2x) + C2 e^(-x) cos(2x) +1/5cos(x) -2/5sin(x)

2.

Cоставляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:

r^2 +0 r - 3 = 0

D=0^2 - 4·1·(-3)=12

Корни характеристического уравнения:

r1 =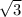

r2 =-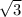

Общее решение однородного уравнения имеет вид:

y- = C1e^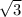 +C2 e^ (-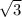) , Ci ∈ R

Рассмотрим правую часть:

f(x) = (4*x+1)*e^(2*x)

Поиск частного решения.

Здесь P(x) = 4•x+1, Q(x) = 0, α = 2, β = 0.

Следовательно, число α + βi = 2 + 0i не является корнем характеристического уравнения.

Уравнение имеет частное решение вида:

y· = (Ax + B)e^(2x)

Вычисляем производные:

y' = A·e^(2x+2(A·x+B)·e^(2x)

y'' = 4(A·x+A+B)·e^(2x)

которые подставляем в исходное дифференциальное уравнение:

y'' -3y = (4(A·x+A+B)·e^(2x)) -3((Ax + B)e^(2x)) = (4·x+1)·e^(2·x)

или

A·x·e^(2x)+4·A·e^(2x)+B·e^(2x) = (4·x+1)·e^(2·x)

Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:

x: A = 4

1: 4A + B = 1

Решая ее, находим:

A = 4;B = -15;

Частное решение имеет вид:

y·=(4x -15)e^(2x)

Таким образом, общее решение дифференциального уравнения имеет вид:

y = y- +y. = C1e^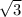 +C2 e^ (-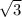) +(4x -15)e^(2x).