с Тренажер №2. Производная степенной функции.
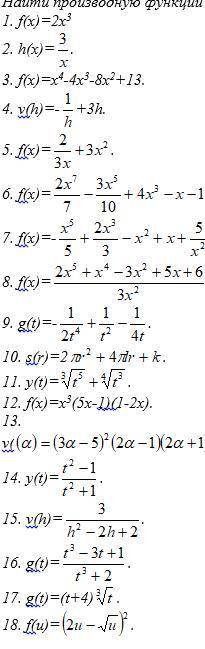
Другие вопросы по теме Алгебра
Популярные вопросы
- Прочитайте рассказ ещё раз. На какие смысловые части его можно разделить?...
2 - Нужно зделать контрольную по химии...
1 - Мураталы куренкеев конспект...
1 - Звести одночлен до стандартного виду 0,02а*10в*30...
1 - 1. Виконати дії: - 1,5 1,5201412,44 +162(3,2-1,7): 0,00329 3. 4:0,2357-...
3 - Кем был Ариант по легенде?...
2 - 1.Следуйте шагам а) (5/8 - 2/5) +3/20 б) 1/8 +(5/9 -1/4) в) 5/6...
3 - Одного чудового осіннього ранку учні нашого класу вирішили піти...
3 - по Алгебре 8 класс.Задание внизу....
3 - Суреттегі тікбұрышты параллелепипед көлемін тап.7 СМ4 см4 СМсмВ...
3
На картинке, которую вы прислали, изображены графики двух функций: f(x) - функции, заданной формулой f(x) = x^n, и ее производной f'(x). Вам нужно найти производную заданной функции.
Для начала, разберемся с понятием производной. Производная функции показывает нам, как быстро изменяется значение функции в каждой конкретной точке ее графика. В математическом обозначении производную функции обозначают f'(x) или dy/dx.
Для нахождения производной степенной функции, вам понадобится знание о правилах дифференцирования степенных функций. Ваша функция f(x) = x^n, где n - некоторое число.
Чтобы найти производную степенной функции, нужно использовать формулу для дифференцирования степенной функции: f'(x) = n * x^(n-1).
Теперь посмотрим на примере, как это работает.
Представим, что у нас есть функция f(x) = x^3. Найдем ее производную по данной формуле.
Производная f'(x) = 3 * x^(3-1) = 3 * x^2. Теперь мы знаем, что производная функции f(x) = x^3 равна f'(x) = 3 * x^2.
Вернемся к картинке, которую вы прислали. На ней изображена функция f(x) = x^n и ее производная f'(x). Оригинальная функция имеет вид кривой линии, а производная функция - прямой линии.
Теперь ваша задача - определить, какой график отображает производную функции f(x) = x^n. Для этого обратите внимание на наклон прямой линии производной функции.
Если вы сравните производную функцию с графиком оригинальной функции, то заметите, что наклон каждой точки прямой линии совпадает с наклоном соответствующей точки кривой линии.
Итак, чтобы определить график, отображающий производную функции f(x) = x^n, нужно найти такую прямую линию, у которой наклон в каждой точке соответствует наклону кривой линии.
Надеюсь, эта пошаговая инструкция поможет вам разобраться с заданием и правильно определить график производной степенной функции. Если у вас есть еще вопросы, не стесняйтесь обращаться. Удачи в решении задания!