1. Алгебра
  2. С тестом тестом теме Степень

С тестом тестом теме "Степень с отрицательным показателем"

ИваПоля ИваПоля    1   01.03.2020 18:26    1

Ответы
kimaleks1977 kimaleks1977  11.10.2020 16:04

1) 12 500;   2) 72;  3) ответ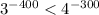 3^{-400} < 4^{-300};  4) 1;  5) 125.

Объяснение:

1.

\Big(\dfrac{4}{5}\Big )^{-2}\cdot (0.05)^{-3} = \dfrac{5^{2} }{4^{2} }\cdot \Big (\dfrac{1}{20}\Big ) ^{-3} = \dfrac{5^{2} }{4^{2} }\cdot \Big (\dfrac{20}{1}\Big ) ^{3} = \\ \\ = \dfrac{5^{2} }{4^{2} }\cdot 4^{3}\cdot 5^{3}= 4\cdot 5^{5} = 4\cdot 3125= 12~500.

2.

\Big(\dfrac{1}{4} \Big)^{-2} \cdot (4.5)^{-3} \cdot \Big(\dfrac{2}{9} \Big)^{-4} =4^{2} \cdot \Big(\dfrac{9}{2} \Big)^{-3} \cdot \Big(\dfrac{9}{2} \Big)^{4}= 16\cdot \dfrac{9}{2} =72.

3.

Сравним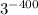  3^{-400} и 4^{-300}

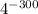
Извлечём корень 100-й степени из обеих чисел, получим

3⁻⁴ и 4⁻³

или

\dfrac{1}{3^{4} }    и    \dfrac{1}{4^{3} }

\dfrac{1}{81 }    и    \dfrac{1}{64} }

\dfrac{1}{81 }< \dfrac{1}{64 }

Поэтому

3^{-400}< 4^{-300}

4.

\dfrac{(x^{4})^{-2} }{x\cdot (x^{-3})^{3} } } = \dfrac{x^{-8} }{x\cdot x^{-9} } } = \dfrac{1 }{x\cdot x^{-1} } } =\dfrac{1 }{1} } } =1

При любом значении х это выражение равно 1.

5.

5⁻⁷ : 5⁻¹⁰ = 1 : 5⁻³ = 5³ = 125

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
maksim22441 maksim22441  21.09.2019 10:40
Знайдіть суму перших десяти членів арифметичної прогресії (xn) якщо х3=-40 ,х5=20...
grgrgrgrgrrhrrhrgrgr grgrgrgrgrrhrrhrgrgr  21.09.2019 10:40
Почему в 20 веке несколько раз менялось название нашей страны?...
energy428 energy428  21.09.2019 10:40
Не выполняя построений, найдите: а) координаты точек пересечения графика функции у = 0,3х – 5 с координатными осями. б) координаты точки пересечения графиков функций у = - 12х +23...
vilkinakarina vilkinakarina  21.09.2019 10:40
Знайдіть перший член та різницю арифметичної прогресії (an),якщо а4=18 ; а7=6...
stigma70 stigma70  21.09.2019 10:40
Третий член арифметической прогрессии равен -3 , а разность её равна -3 , сколько членов этой прогрессии нужно взять , чтобы их сумма была равна -15 ?...
ераврлга ераврлга  21.09.2019 10:40
Знайдіть різницю арифметичної проекції 7; 5; 3; іть...
pecheintsynak pecheintsynak  25.09.2019 15:10
Выполните действие: (2а-3б)(2а+3б)-4а²...
egorjanov2200 egorjanov2200  25.09.2019 15:10
Выраж. (3а-б)(4б-+3а)в квадрате и ещё 4аб-а(2б-а)...
mushdal mushdal  25.09.2019 15:10
Два велосипедиста выезжают одновременно из пункта а и направляются в пункт в, удаленный от а на 180 км. скорость первого велосипедиста на 1 км/ч больше скоро¬сти второго, поэтому первый...
ВероникаКарпова ВероникаКарпова  25.09.2019 15:10
Набір інтервью молодого журналіста миколи складаеться із ручки та блокноту . яка вартість цього набору , якщо 2 ручки та 4 блокноти коштують 15 грн , а 5 ручок та 3 блокнота -16грн...

Популярные вопросы