с сором по алгебре, от 1. Решите неравенства:
+3x+6<0
b) -r² +5x-16>0
2. Решите систему неравенств:
[18-3x <0;
x²-x-12 20.
[5]
[5]
[6]
Другие вопросы по теме Алгебра
Популярные вопросы
- Зделайте ответы кратко: 1 quel jour la maman de julie a écrit...
3 - 1. найдите гипотенузу прямоугольного треугольника, катеты которого...
3 - Как высчитать сколько я буду весть на луне? ...
3 - Составить предложения с этими крылатыми выражениями...
2 - 40 + ! нужно написать 5 предложений(можно больше) в passive...
3 - 2. середня лінія трапеції дорівнює 2,4 дм і ділиться діагоналлю...
2 - А) заполнить пропуски, бусоединить стрелкамигражданская войнаноябрь...
3 - Нужно написать 5 маленьких текстов про город в разных стилях...
3 - (таблица6) я не понимаю задали и не объяснили...
3 - Радиус одной окружности равен 5, другой 1. во сколько раз первая...
1
а)
По теореме Виета :
б)
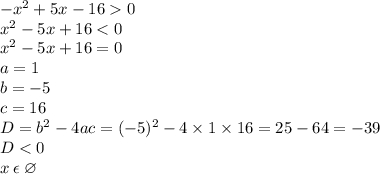
2.