с системой тригонометрических уравнений
sinx•cosy = -3/4
cosx•siny = 1/4
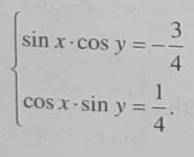
Другие вопросы по теме Алгебра
Популярные вопросы
- Как изменить уравнение так чтобы корень остался прежним...
3 - Язык составьте и запишите диалог из 3-4 реплик дома(разговор по телефону)...
1 - Перевести на язык: become healthy,see interesting places whech tourists very...
1 - Как перевести 18000кдж в дж.и желательно с обьяснениями. я на контрольной...
2 - Гек сварил на костре 2литра каши и разлил эту кашу поровну в 3одинаковые кателка,сколько...
1 - Знайти d(y) 1. y=5/x+7 2.y=3/x+4/x+3 y=x-5/x-1...
3 - Небольшое сообщение об одном из полезных растений...
3 - Выполни деление с объяснением. 564: 4 471: 3 296: 2 792: 4...
2 - Собственная скорасть катера 30км/ч а скорость течение реки 22км/ч.катер 1,2...
1 - Найти в цепочке шесть слов goodogoatwelvelevenora...
2
Сложим и вычтем оба уравнения и получим равносильную систему:
Сложим уравнения и найдем x
Теперь выразим y
ответ: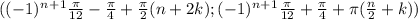 n,k ∈ Z
n,k ∈ Z