С РЕШЕНИЕМ При каких значениях х функция y = 2x + 3/4 - 6x - 5/3 принимает отрицательное значения?

1) х > -11/48

2) х > 29/18

Объяснение:

Отрицательные значения функция принимает при условии, что у(х) < 0. Тогда: (маленькие цифры возле дробей – доп. множители)

1) если пример выглядит как 1) на фотографии:

2х + 3/4³ - 6х - 5/3⁴ < 0

-4х < 20/12 - 9/12

-4х < 11/12

х > -11/48

2) если пример выглядит как 2) на фотографии:

(2х + 3)/4³ - (6х - 5)/3⁴ < 0

(6х + 9 - 24х + 20)/12 < 0

(-18х + 29)/12 < 0

-18х + 29 < 0

-18х < -29

х > 29/18

при x ∈ (; +∞)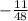

Объяснение:

При x ∈ (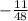; +∞) функция 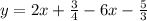принимает отрицательные значения