с решением неопределенных интегралов!
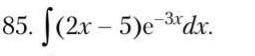
Другие вопросы по теме Алгебра
Популярные вопросы
- с биологией Нужно дать характеристику цветку Мать-и-мачеха, по плану:...
3 - 2. Вычислите, применяя переместительное и сочетательное свойства...
1 - ответьте на вопросы по рассказу ревизор 1. Кто подсказал сюжет комедии...
1 - Нужно распределить слова в таблицу: (не)зависимо интеллекта деятельностьприродувычисленияпринципиально(ни)какого...
2 - КТО ЗНАЕТ МАТЕМАТИКУ НА ОТЛИЧНО...
2 - Look at the map. Then listen and choose the correct migration route...
1 - Вставьте пропущенные слова...
3 - Сравни выражение каждого столбика...
2 - Морфологический разбор (третье)...
3 - Цели восстания на Мангыстау...
2
по частям:
по формуле: