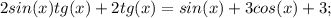 с решением данного уравнения.
с решением данного уравнения.
Другие вопросы по теме Алгебра
Популярные вопросы
- АВ — ось симметрии фигуры. Достройте фигуры....
3 - Масса одного литра морской воды составляет 1 кг 25 Какова масса 4 л воды?...
2 - Постройте треугольники АВС и MKD по координатам их вершин. А (1, 3), В...
2 - Запишите выражения: сумма 362 и а, разность т и произведения 5 и т ....
1 - Угол В — прямой, АВ = 30 мм, ВС = 20 мм. Достройте треугольник АВС до...
1 - Выделите цветным карандашом стороны многоугольников, образующие прямой...
3 - Найди и отметь места в зрительном зале, соответствуют билетам....
1 - Заполните таблицу значений выражения 5 • х....
3 - Для новогоднего праздника купили 32 игрушки: 24 шара и хлопушки. Запишите...
3 - Рассмотрите рисунок. Заполните схемы числами и запишите краткие пояснения...
3
ОДЗ x≠ (π/2) + πn, n∈Z.
Домножим уравнение на cos(x)≠0,
1) sin(x) + cos(x) + 1 = 0
или
2) sin(x) - 3cos(x) = 0.
Решаем 1)
sin(x) + cos(x) = -1,
или
эта серия решений не входит в ОДЗ.
или
Решаем 2)
sin(x) - 3cos(x) = 0,
sin(x) = 3cos(x),
делим на cos(x)≠0,
sin(x)/cos(x) = 3,
tg(x) = 3,
x = arctg(3) + π·m
ответ. x = -π + 2πk, k∈Z или x=arctg(3) + πm, m∈Z.