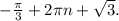С производных высших порядков найти экстремум функции y=x-2sin(x).
Другие вопросы по теме Алгебра
Популярные вопросы
- Написать сочинение-настроение на тему я видел !...
2 - Инна испекла пирожки с повидлом и угостила их ими своих друзей...
1 - Если соединить последовательно два одинаковых электрический...
1 - Два абонента в течение 30 минут должны позвонить по одному и...
2 - Fill in the correct form of the verb to rain выбрать правильный...
1 - Чому ящірка може розмножуватися на суші...
2 - Решите : две художницы расписывают ткань на занавес в театр....
1 - 7rabotnikow nujno 14 chasow adin rabotnik zabolel skolko skolcho...
1 - Треугольник с катетом 43 см и противолежащим углом 60.все боковые...
3 - Охарактеризуйте влияние первой мировой на положение россии...
1
ответ: точки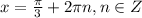 - точки минимума; в этих точках функция равна
- точки минимума; в этих точках функция равна 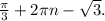 Точки
Точки 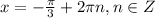 - точки максимума; в этих точках функция равна
- точки максимума; в этих точках функция равна