с поиском корней, принадлежащих промежутку. Тригонометрия!
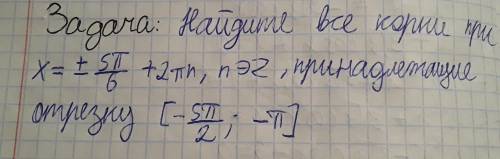
Другие вопросы по теме Алгебра
Популярные вопросы
- Слегка затворить дверь, сделать ручным дикое животное, загородить дорогу. с правописанием...
3 - Подготовьте сообщение об одном из памятников природы крыма...
2 - Слова в которых спрятались животные! например: скорость- кот и крот...
2 - Составить предложение на ! нужно 6-10 предложений на тему: книги которые я читаю...
3 - Використовуючи етикетні форми складіть діалог розмова в автобусі (учень що запізнюється...
3 - Если числитель роби уменьшить на 20% то на сколько процентов надо изменить знаменатель...
2 - Почему печалился царь салтан из сказки...
1 - ответить на 3 вопроса ex. 91 which of the following entertainment activities...
2 - 1.пусть а - множество треугольников с углом 450, в - множество равнобед-ренных...
1 - Друг! реши мне еще! автомобиль за 10 мин проезжает 109.2 км. какова его средняя...
3
неравеством
на этом промежутке нет целых чисел.
Получаем
показать на числовой окружности.
рисунок