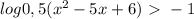 С одз и методом интервалов
С одз и методом интервалов
Другие вопросы по теме Алгебра
Популярные вопросы
- Reading A novel in this text from Great Expectations a boy called...
3 - II. Завдання: розкрити дужки, використовуючи ThePresent Perfect...
1 - Изучение свойств раствора хлороводородной кислоты Лабораторная работа...
2 - У трикутника ABC AC=5√2 см, C=30⁰, B=45⁰. Знайти довжину сторони...
1 - Значение пословицы «Досыта не накормим, а с голоду не уморим»?...
3 - Задания: 1. Опишите историю строительства Турксиба. 2. Найдите дополнительный...
3 - Укажите СПП с придаточным обстоятельственным. А Сердце предчувствовало,...
1 - Адам озинин киялы аркылы изденеди дуние озгертуге,жангыртуга тырысады...
3 - Являются ли уравнения равносильными? Если да, то сформулируйте,...
2 - Укажіть іб, за до якого можна надати позитивного заряду металевій...
2
ответ: хЄ ( 1 ; 2 ) U ( 3 ; 4 ) .
Объяснение:
log₀,₅( x² - 5x + 6 ) > - 1 ; ОДЗ : x² - 5x + 6 > 0 ; D = 1 > 0 ;
рішаємо нерівність методом інтерв. x₁ =2 ; x₂ = 3 ; xЄ (- ∞ ;2)U(3 ;+ ∞ ).
log₀,₅( x² - 5x + 6 ) > log₀,₅0,5⁻¹ ;
a = 0,5 < 1 ( спадна ф - ція ) ;
{ x² - 5x + 6 < 2 , ⇒ { x² - 5x + 4 < 0 ,
{ x² - 5x + 6 > 0 ; { x² - 5x + 6 > 0 ; рішаємо нерівності :
1) x² - 5x + 4 < 0 ; D = 9 > 0 ; x₁ = 1 ; x₂ = 4 ; хЄ ( 1 ; 4 ) ;
2) x² - 5x + 6 > 0 ; D =1 > 0 ; x₁ = 2 ; x₂ = 3 ; xЄ (- ∞ ;2 )U( 3 ;+ ∞ ) .
Зобразимо проміжки на одній числовій прямій і запишемо
розв"язки : хЄ ( 1 ; 2 ) U ( 3 ; 4 ) .